Помогите решить 2 задачи ,ОООООЧЕНЬ СРОЧНО

Ответы
Ответ:
Доказано:
70) ΔABC = ΔKNM; AN = KB;
71) ΔABC = ΔCDA.
Объяснение:
Требуется:
70) Доказать: ΔABC = ΔKNM; AN = KB;
71) Доказать: ΔABC = ΔCDA.
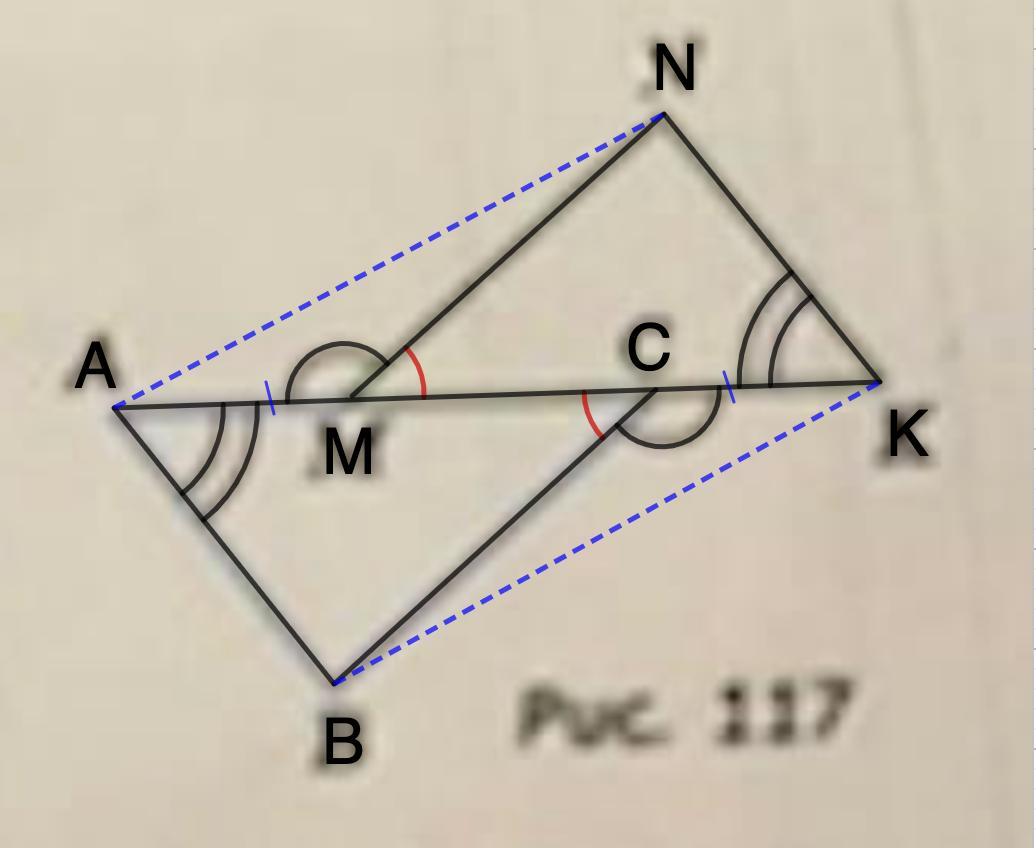
70.
Дано: ∠BAC = ∠NKM; ∠AMN = ∠KCB;
AM = KC.
Доказать: a) ΔABC = ΔKNM; б) AN = KB.
Доказательство:
а)
1. Рассмотрим ΔABC и ΔKNM.
АС = AM + MC
MK = KC + MC
AM = KC (условие)
- Если правые части равенства равны, то равны и левые.
⇒ АС = МК
∠BAC = ∠NKM (условие)
- Смежные углы равны в сумме 180°.
∠АСВ = 180° - ∠АМN (смежные)
∠MKN = 180° - ∠BCK (смежные)
∠AMN = ∠KCB (условие)
⇒ ∠АСВ = ∠MKN
ΔABC = ΔKNM (по стороне и двум прилежащим углам; 2 признак)
б)
2. Рассмотрим ΔABC и ΔCDA.
ΔABC = ΔKNM (п.1)
- Если треугольники равны, то равны их соответственные элементы.
⇒ MN = BC
∠AMN = ∠KCB (условие)
AM = KC (условие)
ΔABC = ΔCDA (по двум сторонам и углу между ними; 1 признак)
⇒ AN = KB (как соответственные элементы)
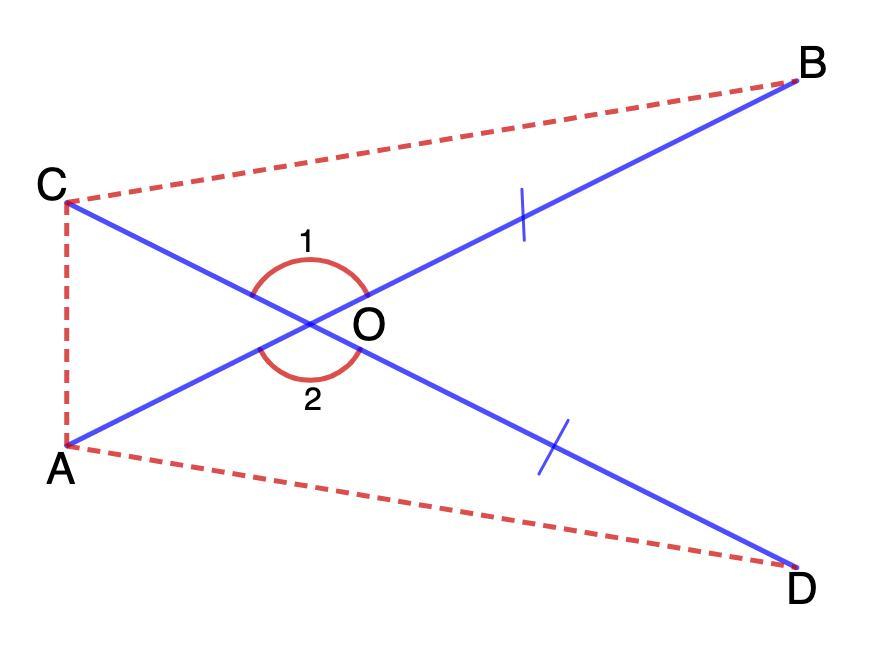
71.
Дано: AB = CD;
AB ∩ CD = O;
OD = OB.
Доказать: ΔАВС = ΔСDA.
Доказательство:
1. Рассмотрим ΔСВО и ΔAOD.
OB = OD (условие)
CO = CD - OD
AO = AB - OB
AB = CD (условие)
⇒ CO = OB
- Вертикальные углы равны.
⇒ ∠1 = ∠2 (вертикальные)
ΔСВО = ΔAOD (по двум сторонам и углу между ними; 1 признак)
⇒ СВ = AD (как соответственные элементы)
2. Рассмотрим ΔАВС и ΔСDA.
СВ = AD (п.1)
AB = CD (условие)
АС - общая.
ΔАВС = ΔСDA (по трем сторонам; 3 признак)