Question

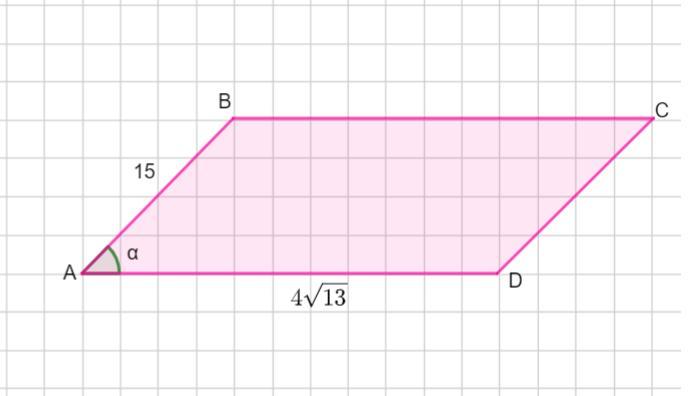
Одна из сторон параллелограмма 15, а другая 4√13 , тангенс одного из углов 2/3, найти площадь параллелограмма

Answer 1

Ответ:

Площадь параллелограмма равна 120 кв. ед.

Пошаговое объяснение:

Пусть дан параллелограмм АВСD , стороны которого АВ= 15,

АD = 4√13 . Значение тангенса положительно, поэтому это тангенс острого угла . ∠А = α и   $tg\alpha =\dfrac{2}{3}$

Найдем площадь параллелограмма по формуле:

$S= a\cdot b\cdot sin\alpha ,$  где a и  b - стороны параллелограмма , α - угол между ними.

Найдем синус угла, воспользовавшись формулой

$1+ ctg^{2} \alpha =\dfrac{1}{sin^{2}\alpha }$

 Если   $tg\alpha =\dfrac{2}{3},$    то    $ctg\alpha =\dfrac{3}{2}$

Тогда получим

$1+ \left(\dfrac{3}{2}\right)^{2} =\dfrac{1}{sin^{2}\alpha };\\\\\dfrac{1}{sin^{2}\alpha }=1+\dfrac{9}{4} ;\\\\\dfrac{1}{sin^{2}\alpha }=\dfrac{13}{4} ;\\\\sin^{2} \alpha =\dfrac{4}{13} ;\\\\sin \alpha =\pm \dfrac{2}{\sqrt{13} }$

Так как α- угол параллелограмма ,  то  $sin\alpha =\dfrac{2}{\sqrt{13} }$

Тогда найдем площадь параллелограмма

$S= 15\cdot 4\sqrt{13} \cdot \dfrac{2}{\sqrt{13} } =60\cdot 2 =120$

Площадь параллелограмма равна 120 кв. ед.