Задание приложено...
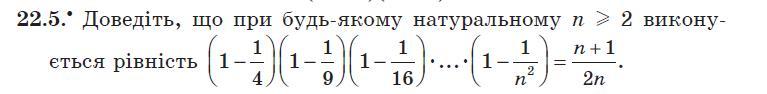
Ответы
Ответ:
Разности в скобках представим как дроби.
Распишем поподробнее множители и сократим одинаковые
От первых двух дробей останется только 2 в знаменателе и 1 в числителе . В последних двух дробях сократится (n-2) в числителе с (n-2) в знаменателе предыдущей дроби , (n-1) в числителе последней дроби с (n-1) в знаменателе предыдущей дроби и (n-1) в знаменателе предпоследней дроби с (n-1) в числителе предыдущей дроби. Ну и n с n² сократятся .Останется только (n+1) в числителе и n в знаменателе .

Ответ:
Согласно методу математической индукции (смотрите фотографии) докажем равенство
Проверим, то что утверждение выполняется для какого-то конкретного n, то есть в данном случае для n = 2. Этот этап проверки еще называю базой математической индукции.
Предположим, что для какого-то k утверждение верно, то есть мы предполагаем, что равенство выполняется.
верно
Теперь докажем, что элемента следующего за k (то есть для k + 1) равенство также выполняется и если это удастся доказать, то есть получить справа и слева одинаковое равенство. Такой переход называют индуктивным.
------------------------------------------------------------------------
а)
б)
----------------------------------------------------------------------------
Так как правую и левую часть тождества
путем равносильных преобразований удалось свести к равному выражению, тогда
первоначально утверждение доказано методом математической индукции.

