Доказать методом математической индукции при натуральных n
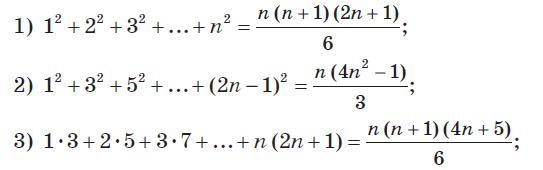
Ответы
Ответ:
1)
- пусть верно
а)
б)
Так как в пункте а) и б) путем равносильных преобразований получилось одно и тоже выражение, то есть а) = б).
Тогда согласно методу математической индукции исходное утверждение доказано.
2)
- пусть верно
а)
б)
в)
г)
Так как в пункте в) и г) путем равносильных преобразований получилось одно и тоже выражение, то есть в) = г).
Тогда согласно методу математической индукции исходное утверждение доказано.
3)
- пусть верно
-----------------------------------------------------------------------------------
а)
б)
-----------------------------------------------------------------------------------
Так как правую и левую часть тождества
путем равносильных преобразований удалось свести к равному выражению, тогда
первоначально утверждение доказано методом математической индукции.

