Question

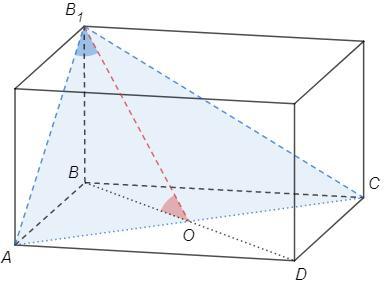
Через диагональ AC квадрата ABCD лежащего в основании прямоугольного паралепида и вершины B1 другого основания параллелепипеда проведена плоскость так, что в сечении получился треугольник АB1С с углом при вершине B1,в два раза большим чем угол между плоскостью сечения и основанием параллелепипеда. Найти угол АB1С.​

Answer 1

Прямоугольный параллелепипед - все грани прямоугольники.

Стороны квадрата равны, AB=BC

=> △ABB1=△CBB1 (по двум катетам)

=> AB1=CB1, △AB1C - равнобедренный

B1O - медиана/высота/биссектриса

Диагонали квадрата перпендикулярны, равны, точкой пересечения делятся пополам.

BO⊥AC, AO=BO=CO

Угол между плоскостями - угол между перпендикулярами к общей прямой.

B1O⊥AC, BO⊥AC => ∠B1OB - угол между плоскостью сечения и основанием.

По условию ∠АB1С =2∠B1OB => ∠АB1O =∠B1OB =ф

Найдем ∠АB1С=2ф

Рассмотрим треугольники AB1O и B1OB

AO/B1O =tgф, BO/B1O=cosф => tgф =cosф =x

tgф^2 +1 =1/cosф^2

x^2 +1 =1/x^2 => x^4 +x^2 -1=0 => x^2 =(√5-1)/2    | x^2>0

cos2ф =2cosф^2 -1 =2*(√5-1)/2 -1 =√5-2

∠АB1С =arccos(√5-2)    ~76,34°