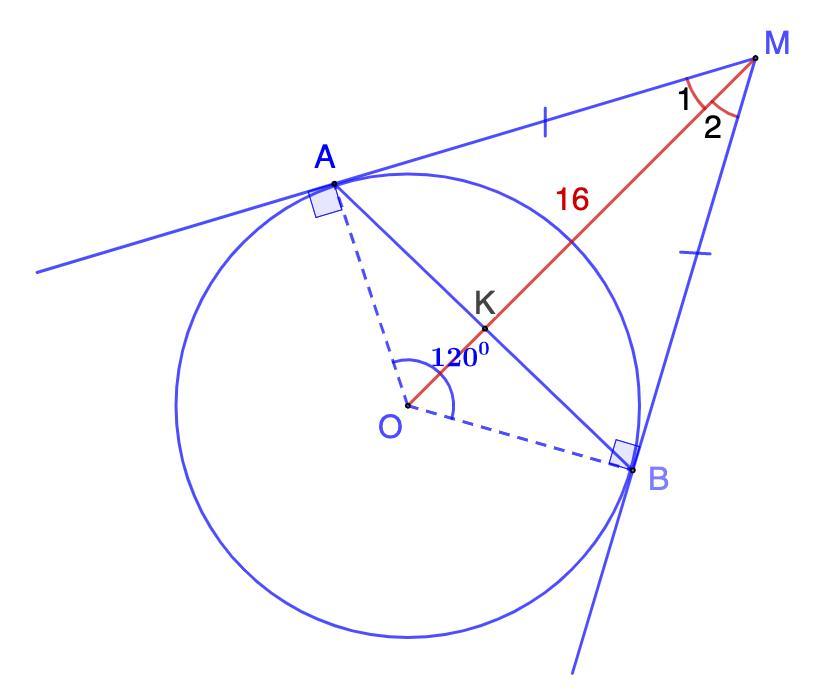
Из точки М к окружности с центром О проведены касательные ма и МБ Найдите расстояние между точками касания A и B если угол АОВ равен 120° и мо равно 16 см
Ответы
Ответ:
Расстояние между точками касания A и B равно 8√3 см.
Объяснение:
Требуется найти расстояние между точками касания A и B.
Дано: Окр.О;
МА и МВ - касательные;
∠АОВ = 120°; МО = 16 см.
Найти: АВ.
Решение:
1. Рассмотрим ΔАМО и ΔОМВ.
- Радиус, проведенный в точку касания, перпендикулярен касательной.
⇒ ΔАМО и ΔОМВ - прямоугольные.
- Отрезки касательных к окружности, проведенные из одной точки, равны.
⇒ МА = МВ.
ОМ - общая.
ΔАМО = ΔОМВ (по гипотенузе и катету)
⇒ ∠АОМ = ∠МОВ = 120° : 2 = 60° (как соответственные элементы)
2. Рассмотрим ΔАМО - прямоугольный;
∠АОМ = 60°
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠1 = 90° - 60° = 30°
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
⇒ АО = МА :2 = 16 :2 = 8 (см)
По теореме Пифогора:
⇒ АМ² = МО² - ОА² = 256 - 64 = 192
АМ = √192 = 8√3 (см)
3. Рассмотрим ΔАМК и ΔКМВ.
АМ = МВ (отрезки касательных)
МК - общая;
- Центр вписанной окружности лежит на биссектрисе угла.
∠1 = ∠2
ΔАМК = ΔКМВ (по 1 признаку)
⇒ АК = КВ; ∠АКМ = ∠МКВ (как соответственные элементы)
- Смежные углы в сумме равны 180°.
⇒ ∠АКМ = ∠МКВ = 180° : 2 = 90°
ΔАМК и ΔКМВ - прямоугольные.
⇒ АК = АМ : 2 = 8√3 : 2 = 4√3 (см) (катет, лежащий против угла 30°)
⇒ АВ = 4√3 · 2 = 8√3 (см)
Расстояние между точками касания A и B равно 8√3 см.