ДАЮ 50 БАЛОВ❗❗❗❗❗❗❗❗СРОЧНО ПЖ ПОМОГИТЕ !!!!!!!!!
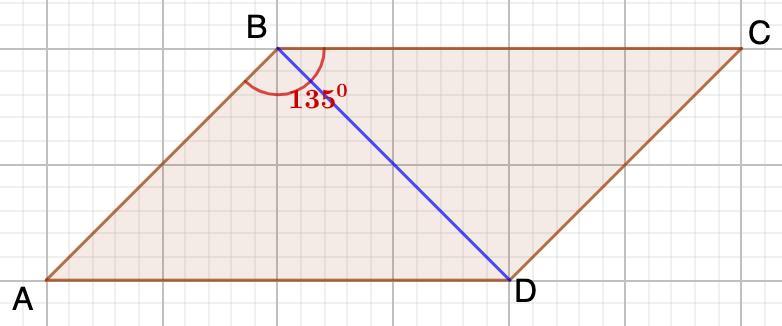
Тупий кут паралелограма дорівнює 〖135〗^°. Діагональ паралелограма ділить його у відношенні 1:2. Знайдіть цю діагональ, якщо периметр паралелограма дорівнює 60 см.
Ответы
Ответ:
Диагональ параллелограмма равна 12,4 см.
Объяснение:
Требуется найти диагональ параллелограмма.
Дано: ABCD - параллелограмм;
∠В = 135°;
∠CBD : ∠ABD = 1 : 2;
P (ABCD) = 60 см.
Найти: BD
Решение:
1. ∠ В = 135°
∠CBD : ∠ABD = 1 : 2.
Пусть ∠CBD = х; тогда ∠ABD = 2х.
х + 2х = 135°
х = 45°
⇒ ∠CBD = 45°; ∠ABD = 2х = 90°.
2. P (ABCD) = 60 см.
- Периметр параллелограмма равен удвоенной сумме смежных сторон.
⇒ P (ABCD) = 2 (АВ + AD) = 60 см.
АВ + AD = 30 см.
3. Рассмотрим ΔABD - прямоугольный.
- Углы параллелограмма, прилежащие к одной стороне, в сумме равны 180°.
⇒ ∠А = 180° - ∠В = 180° - 135° = 45°
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠ADB = 90° - ∠A = 90° - 45° = 45°
ΔABD - равнобедренный.
⇒ АВ = ВD
Пусть АВ = ВD = х см, тогда AD = (30 - x) см.
По теореме Пифагора:
AB² + BD² = AD²
x² + x² = (30 - x)²
2x² = 900 - 60x + x²
x² + 60x - 900 = 0
x₂ - не подходит, так как длина не может быть числом отрицательным.
⇒ АВ = ВD = 30(√2 - 1) см ≈ 12,4 см
Диагональ параллелограмма равна 12,4 см.