Предмет: Алгебра,
автор: superredbear
помогите пожалуйста
Приложения:
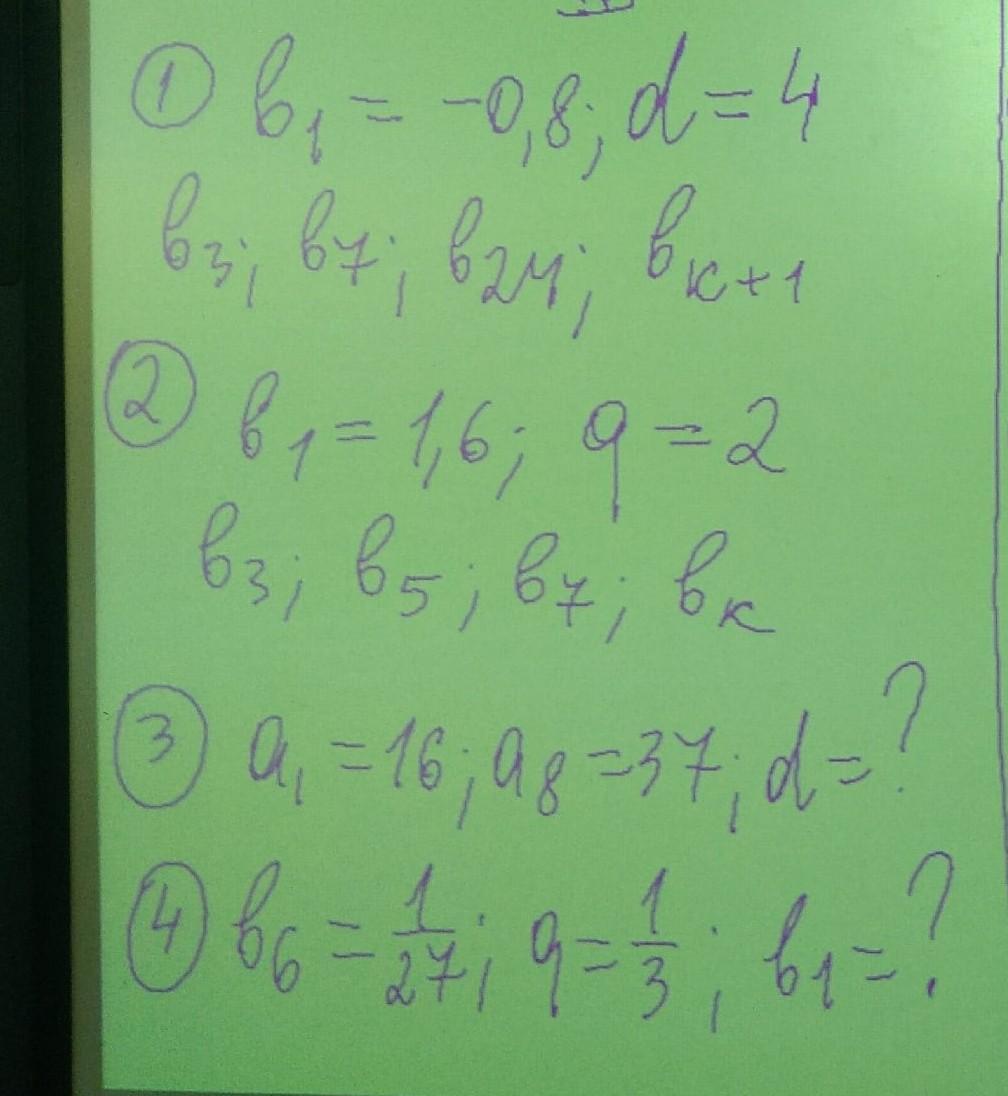
Ответы
Автор ответа:
3
Ответ:
Используем формулу n-ых членов арифм. и геом. прогрессий .
1) Арифметическая прогрессия :
2) Геометрическая прогрессия: .
3) Арифметическая прогрессия .
4) Геометрическая прогрессия.
superredbear:
спасибо
пожалуйста
Похожие вопросы
Предмет: Английский язык,
автор: kurmanovaybek
Предмет: Русский язык,
автор: lopoiu
Предмет: Русский язык,
автор: elyadiana
Предмет: Математика,
автор: kamillla1
Предмет: Математика,
автор: Аноним