Question

Помогите с интегралами, прошу! Очень надо!

Answer 1

Ответ:

искомый объем заданного тела вращения равен    $\displaystyle \boldsymbol {\frac{\pi }{2} }$

Пошаговое объяснение:

Формула для расчета объема тела вращения

$\displaystyle V=\pi \int\limits^a_b {f^2(x)} \, dx$

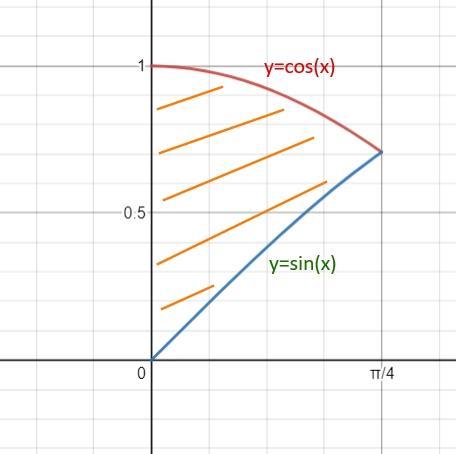
Сначала сделаем чертеж.

По чертежу видно, что объем нашего тела вращения  будет равен разности объемов двух тел.

$\displaystyle V=\pi \int\limits^a_b {\bigg(y_1^2(x)-y^2_2(x)\bigg)} \, dx$

За у₁(х) мы берем функцию, график которой лежит "выше" на чертеже.  

у₁(х) = cos(x)

Пределы интегрирования у нас заданы в условии  от 0 до $\pi /4$ .

Будем пользоваться формулами

$\displaystyle sin^2(x) = \frac{1}{2} - \frac{1}{2}cos(2x)\\\\\\cos^2(x) = \frac{1}{2} +\frac{1}{2}cos(2x)$

Формула для расчета нашего объема

$\displaystyle V=\pi \int\limits^a_b {\bigg(cos^2(x)-sin^2(x)\bigg)} \, dx$

Интеграл громоздкий, поэтому я не буду таскать везде  $\pi$.

Добавим его в самом конце..

Сначала будем разбираться с sin²(x) , потом с cos²(x)

Итак, поехали.

$\displaystyle \int\limits^{\pi /4}_0 {(cos^2(x) -sin^2(x))} \, dx =-\int\limits^{\pi /4}_0 {sin^2(x)} \, dx +\int\limits^{\pi /4}_0 {cos^2(x)} \, dx$

Оставим пока в покое второй интеграл, разберемся с первым.

Заметим, что при замене переменных меняются пределы интегрирования.

$\displaystyle -\int\limits^{\pi /4}_0 {sin^2(x)} \, dx =-\frac{1}{2} \int\limits^{\pi /4}_0 {} \, dx+\frac{1}{2} \int\limits^{\pi /4}_0 {cos(2x)} \, dx =\\\\\\=-\frac{x}{2} \bigg|_0^{\pi /4}+\frac{1}{2} \left[\begin{array}{ccc}u=2x;&du=2dx\\u_1=0&u_2=\pi /2\\\end{array}\right] =-\frac{\pi }{8} +\frac{1}{4} \int\limits^{\pi /2}_b {cos(u)} \, du =$

$\displaystyle = -\frac{\pi }{8} +\frac{sin(u)}{4} \bigg |_0^{\pi /2}=-\frac{\pi }{8} +\frac{1}{4}$

Запомнили, чему равен первый интеграл и аналогичным образом считаем второй интеграл

$\displaystyle \int\limits^{\pi /4}_0 {cos^2(x)} \, dx =\frac{1}{2} \int\limits^{\pi /4}_0 {} \, dx +\frac{1}{2} \int\limits^{\pi /4}_0 {cos(2x)} \, dx =\\\\\\=\frac{x}{2} \bigg |_0^{\pi /4}+\frac{1}{2} \left[\begin{array}{ccc}s=2x&ds=2dx\\s_1=0&s_2=\pi /2&\\\end{array}\right] =\\\\\\=\frac{\pi }{8} +\frac{1}{4}\int\limits^0_{\pi /2} {cos(s)} \, ds =\frac{\pi }{8} +\frac{sin(s)}{4} \bigg |_0^{\pi /2}=\frac{\pi }{8} +\frac{1}{4}$

Теперь замечательно сложим значения двух интегралов

$\displaystyle ==-\frac{\pi }{8} +\frac{1}{4} +\frac{\pi }{8} +\frac{1}{4} =\boldsymbol {\frac{1}{2} }$

Вспоминаем про формулу объема и оставленный без присмотра  $\pi$.

Возвращаем все на свои места и получаем искомый объем заданного тела вращения.

$\displaystyle V=\pi *\frac{1}{2} =\boldsymbol {\frac{\pi }{2} }$