по графику скорости построить график перемещения. Записать уравнение движения
Помогите пожалуйста 100 баллов даю
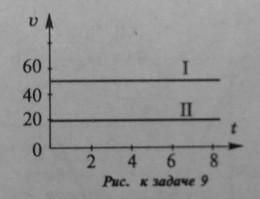
Ответы
Ответ:
ОбВ физике и математике используют три способа подачи информации о связи между различными величинами: а) в виде формулы, например, s =v ∙ t; б) в виде таблицы; в) в виде графика (рисунка).
Зависимость скорости от времени v(t) - график скорости изображается с помощью двух взаимно перпендикулярных осей. Вдоль горизонтальной оси будем откладывать время, а по вертикальной - скорость (рис. 14.1). Надо заблаговременно продумать масштаб, чтобы рисунок не был слишком большим или слишком малым. У конца оси указывают букву, которая является обозначением численно равна площади заштрихованного прямоугольника abcd величины, что на ней откладывается. Возле буквы указывают единицу измерения этой величины. Например, возле оси времени указывают t, с, а возле оси скорости v(t), мес. Выбирают масштаб и наносят деления на каждую ось.
Рис. 14.1. График скорости тела, равномерно движущегося со скоростью 3 м/сек. Путь, пройденный телом со 2-й по 6-ю секунды,
Изображение равномерного движения таблицей и графиками
Рассмотрим равномерное движение тела со скоростью 3 м/с, то есть числовое значение скорости будет постоянным в течение всего времени движения. Сокращенно это записывают так: v = const (константа, то есть постоянная величина). В нашем примере она равна трем: v = 3 . Вы уже знаете, что информацию о зависимости одной величины от другой можно подавать в виде таблицы (массива, как говорят в информатике):
Из таблицы видно, что во все указанные моменты времени скорость равна 3 м/сек. Пусть масштаб оси времени 2 кл. = 1 с, а оси скорости 2 кл. = 1 м/сек. График зависимости скорости от времени (сокращенно говорят: график скорости) приведены на рисунке 14.1.
С помощью графика скорости можно найти путь, который тело проходит за определенный интервал времени. Для этого нужно сопоставить два факта: с одной стороны, путь можно найти, умножив скорость на время, а с другой - произведение скорости на время, как видно из рисунка - это площадь прямоугольника со сторонами t и v.
Например, со второй до шестой секунды тело двигалось в течение четырех секунд и прошло 3 м/с ∙ 4 с = 12 м. Это площадь прямоугольника аbсd, длина которого равна 4 с (отрезок ad вдоль оси времени) и высота 3 м/с (отрезок аb вдоль вертикали). Площадь, правда, несколько необычная, поскольку измеряется не в м 2 , а в г. Следовательно, площадь под графиком скорости численно равна пройденному пути.
График пути
График пути s(t) можно изобразить, используя формулу s = v ∙ t, то есть в нашем случае, когда скорость составляет 3 м/с: s = 3 ∙ t. Построим таблицу:
Вдоль горизонтальной оси снова откладывают время (t, с), а вдоль вертикальной - путь. Возле оси пути пишем: s, м (рис. 14.2).
Определение скорости по графику пути
Изобразим теперь на одном рисунке два графика, которые будут соответствовать движениям со скоростями 3 м/с (прямая 2) и 6 м/с (прямая 1) (рис. 14.3). Видно, что чем больше скорость тела, тем круче линия точек графика.
Существует и обратная задача: имея график движения, нужно определить скорость и записать уравнение пути (рис. 14.3). Рассмотрим прямую 2. От начала движения и до момента времени t = 2 с тело прошло путь s = 6 м. Следовательно, его скорость: v = = 3 . Выбор другого интервала времени ничего не изменит, например, на момент t = 4 с путь, пройденный телом от начала движения, составляет s = 12 м. Отношение опять равна 3 м/сек. Но так и должно быть, поскольку тело движется с постоянной скоростью. Поэтому проще всего было бы выбрать интервал времени 1 с, ведь путь, пройденный телом за одну секунду, численно равна скорости. Путь, пройденный первым телом (график 1) за 1 с, равна 6 м, то есть скорость первого тела равна 6 м/сек. Соответствующие зависимости пути от времени в этих двух тел будут:
s 1 = 6 ∙ t и s 2 =3 ∙ t.