Предмет: Алгебра,
автор: parkurshik05
найти первообразную даю 100 баллов
Приложения:
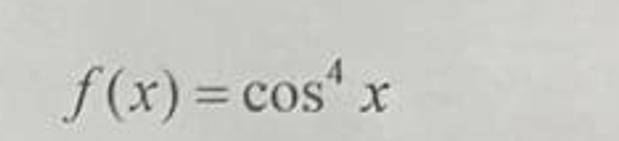
Ответы
Автор ответа:
0
Решение задания находится во вложении.
Приложения:

Автор ответа:
0
Ответ:
Объяснение:
Сначала преобразуем функцию
теперь найдем первообразную
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: elenazyukanova1
Предмет: Українська література,
автор: Вероника200555
Предмет: Математика,
автор: Leon73388