Помогите срочно!!
С объяснением)

Ответы
Ответ:
см^2
Пошаговое объяснение:
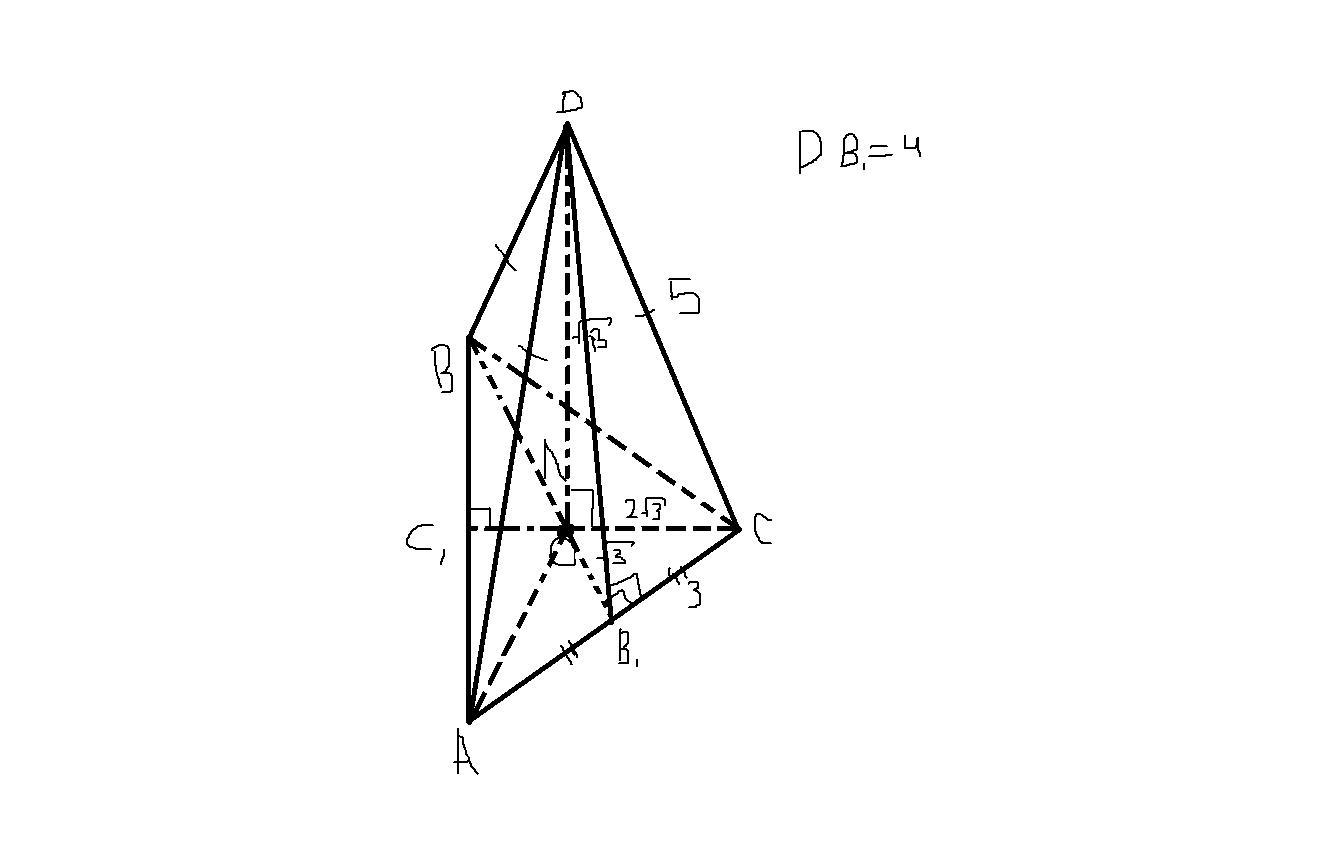
1) Имеется правильная треугольная пирамида DABC (ABC - основание). Точка O - центр ABC, т. е. DO - высота пирамиды. Отметим, что т. О - точка пересечения высот ΔABC. Обозначим основания этих высот как B1 и C1 (см. рис.)
2) По т. Пифагора для ΔDOC (∠O = 90°, т. к. DO - высота):
В правильном треугольнике высоты точкой пересечения делятся в соотношении 2:1 (от вершины), значит BB1 = CC1 = 1.5*OC = 3√3 и OC1 = OB1 = √3. Также OA = OC = 2√3
3) OA = OC (п. 2) ⇒ ΔAOC - равнобедренный и AB1 = CB1 (OB1 - высота; высота в равноб. треугольнике - его медиана)
Проведём DB1. Так как пирамида правильная, её боковые рёбра равны, т. е. AD = DC, а так как AB1 = CB1, то DB1 - высота ΔADC
4) Для ΔB1OC по т. Пифагора , B1C = 3
AC = 2*B1C = 6.
Для ΔDB1C по т. Пифагора , DB1 = 4
(площади равны, так как треугольники равны по 3-м сторонам)
5) (AC = 6 - п. 4, BB1 = 3√3 - п. 2)
Площадь полной поверхности: (см^2)