ТОТ КТО ПОДРОБНО ОБЪЯСНИТ ЭТО ПОЛУЧИТ 100 БАЛЛОВ!!!
∫sinxcosxdx = ∫0,5sin2xdx = ∫0,25sin2xd(2x) = -0,25cos2x + C
я запутался из-за этого:
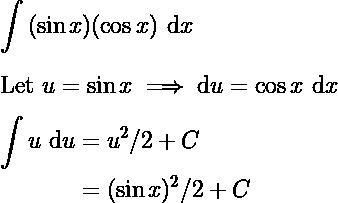
Ответы
Объяснение через du:
Мы делаем замену u=sinx. Тогда наш интеграл превращается в такой:
Проблема в том, что не очень понятно, что делать с этим u. Интегрируем мы по x (т.к. в конце приписано dx).
Нам нужно преобразовать выражение так, чтобы в конце было приписано du.
Т.к. u = sinx, возьмем производную от обеих частей:
du/dx = (d/dx)sinx
du/dx = (d*sinx)/dx
Производная от синуса равна косинусу, поэтому
du/dx = cosx
Домножаем обе части на dx:
du = cosx*dx
И это победа! Т.к. u=sinx, а cosx * dx = du, мы можем обе эти части в исходном интеграле заменить, и получим: =
+С (т.к. интеграл от u^n =
+ С)
Делаем обратную замену:
(u^2)/2 + C = ((sinx)^2)/2 + C
----------------
Как в тексте:
∫sinxcosxdx
Применим формулу для произведения синуса и косинуса: sina * cosa = (sin(a-a) + sin(α+a))/2 = (sin0 + sin(2a))/2 = (sin2a)/2.
Тогда исходный интеграл можно записать как ∫0.5sin2xdx
Та же проблема: в аргументе функции у нас стоит 2x, а интегрируем просто по х. Но мы можем коэффицент (0.5) поделить на 2, чтобы получить d(2x). Так и делаем:
∫0.5sin2xdx = ∫0.25 * sin(2x) * d(2x)
Производная от sinx = -cosx, а 0.25 не трогаем, т.к. это коэффицент. Получаем
0.25 * (-cos2x) + C = -0.25*cos2x + C
----------------
И тот ответ, что ты вписал в самом вопросе, и тот, что во вложении, являются правильными. Это можно проверить, если взять производную от них