Question

помогите 100 баллов ​

Answer 1

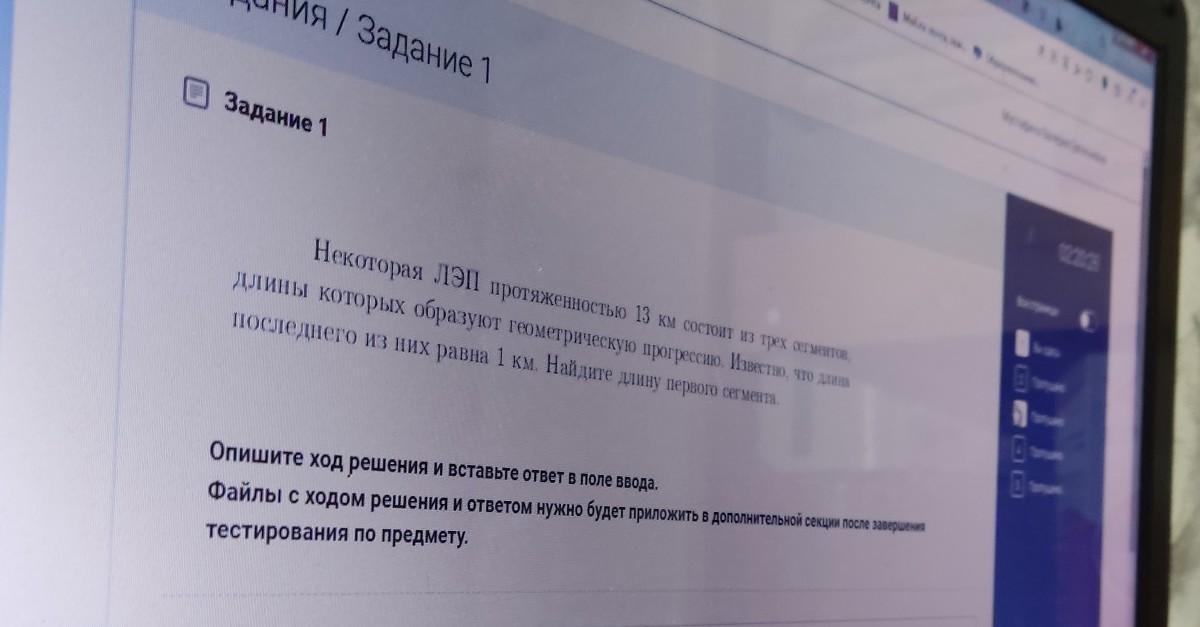
поскольку речь о геометрической прогрессии, то сумма трех первых ее членов составляет

sn=b₁*(qⁿ-1)/(q-1)

s₃=b₁*(q³-1)/(q-1)=b₁*(q-1)(q₂+q+1)/(q-1)=b₁*(q²+q+1)

b₁*(q²+q+1)=13

три ее сегмента это  b₁; b₁q; b₁q², причем b₁q²=1, откуда  b₁=1/q²;

т.о., (q²+q+1)/q²=13;

q²+q+1=13q²; 12q²-q-1-0; q=(1±√(1+48))/24; q₁=8/24=1/3;  q₂-6/24=-1/4=-- не подходит по смыслу задачи.

тогда длина первого сегмента равна  b₁=1/q²=1/(1/9)=9 /км/;

Ответ  9 км

Answer 2

Ответ:   9 км .

Три сегмента линии электропередач образуют геометрическую

, значит их длины равны  $b_1\ ,\ b_1q\ ,\ b_1q^2$  .

Общая длина равна  $b_1+b_1q+b_1q^2=13\ \ \Rightarrow \ \ b_1\, (1=q+q^2)=13$  .

Длина третьего сегмента равна   $b_1q^2=1\ \ \Rightarrow \ \ \ b_1=\dfrac{1}{q^2}$  .  Тогда

$\dfrac{1}{q^2} \cdot (1+q+q^2)=13\ \ \Rightarrow \ \ \ 1+q+q^2=13q^2\ \ ,\ \ 12q^2-q-1=0\ ,\\\\\\D=b^2-4ac=1^2+4\cdot 12=49\ ,\ \ q_1=\dfrac{1-7}{24}=-\dfrac{1}{4} < 0\ \ ne\ podxodit\ ,\\\\q_2=\dfrac{1+7}{24}=\dfrac{1}{3}$

Длина первого сегмента равна   $b_1=\dfrac{1}{q^2}=\dfrac{1}{(\frac{1}{3})^2}=\dfrac{1}{\frac{1}{9}}=9$    (км) .