Предмет: Математика,
автор: Астра8000
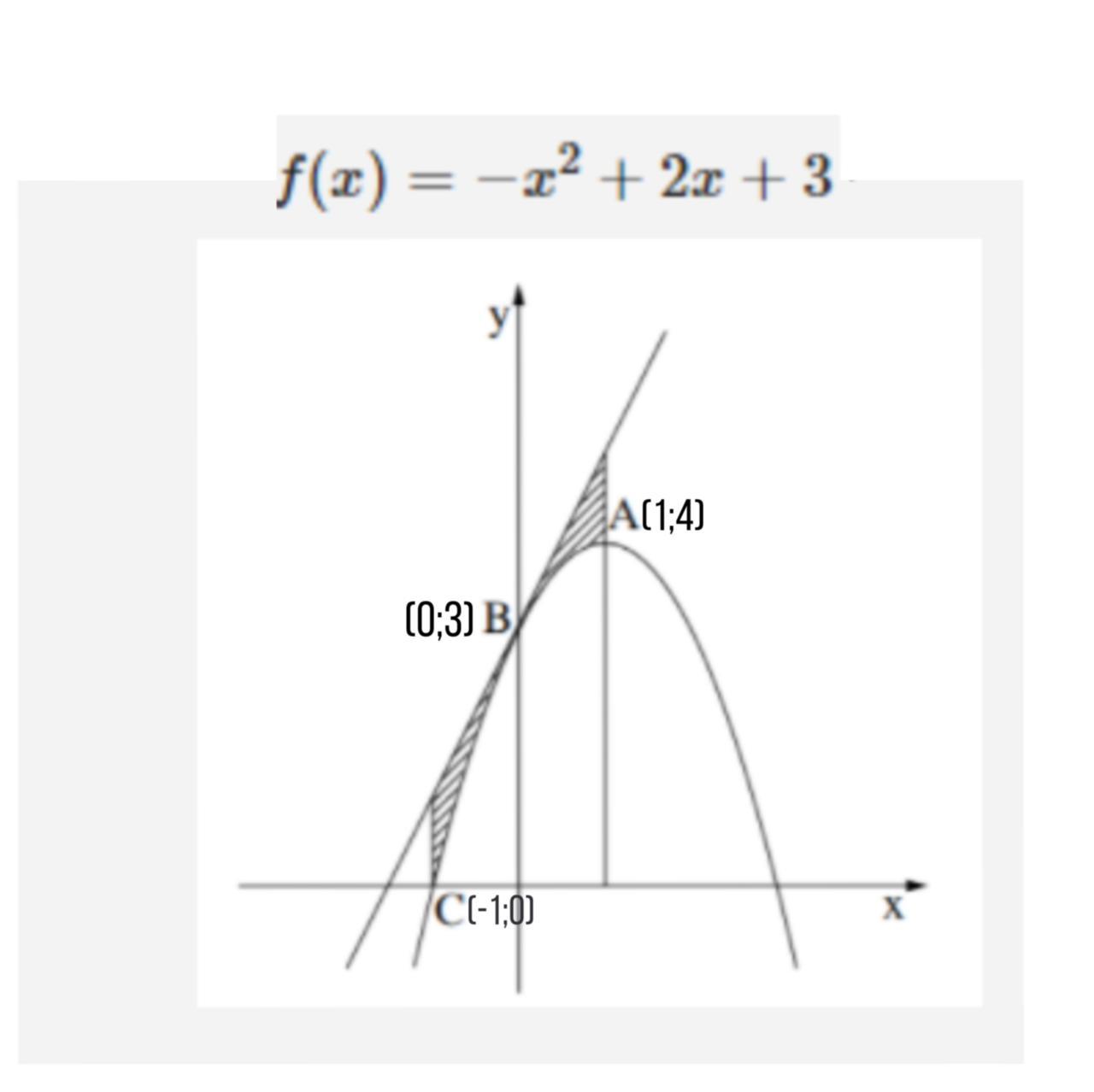
Срочно! ИНТЕГРАЛЫ. ЗАДАЧА НА КАРТИНКЕ . Нужно найти площадь заштрихованной фигуры
Приложения:
Ответы
Автор ответа:
1
Прямая y=kx+b касается f(x)=-x^2+2x+3 в точке х0=0, f(x0)=3
Уравнение касательной в этой точке
y=f'(x0)(x-x0)+f(x0)
f'(x)=-2x+2, f'(0)=2 => y=2(x-0)+3
y=g(x)=2x+3 - уравнение прямой
Парабола проходит через точки А, В, С
F(x)=
G(x)=x^2+3x
Тогда площадь фигуры S = (G(1)-G(-1))-(F(1)-(F(-1))
G(1)-G(-1) = 1+3-1+3=6
F(1)-F(-1) = -1/3+1+3-(1/3+1-3)=16/3
S = 6-16/3 = 2/3
Похожие вопросы
Предмет: Русский язык,
автор: kartakaewanata
Предмет: Русский язык,
автор: виолета112
Предмет: Русский язык,
автор: кеек4
Предмет: Биология,
автор: kotandpusa0617
Предмет: Математика,
автор: zhauharsurtaeva