Предмет: Математика,
автор: Аноним
математика математика математика математика математика математика математика математика математика математика математика математика
Приложения:
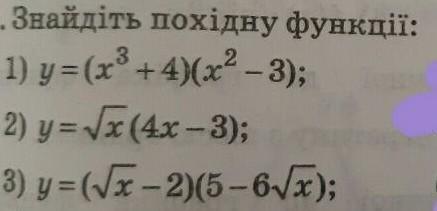
Ответы
Автор ответа:
8
Ответ:
1)
y=(x³+4)(x²-3)
y=x⁵-3x³+4x²-12
y'=5x⁴-9x²+8x
2)
y=√(x)*(4x-3)
y=x^(1/2)*(4x-3)
y=4x^(3/2)-3x^(1/2)
y'=6x^(1/2)-3/2x^(-1/2)
y'=6√(x)-3/(2√x)
3)
y=(√(x)-2)*(5-6√(x))
y=5√(x)-6x-10+12√(x)
y'=5/(2√x)-6+6/√(x)
помогите у меня информатика
круто
с чем помочь?
задание в профиле????
здравствуйте у меня есть задание по информатике
Автор ответа:
8
Ответ:
Применяем правило дифференцирования произведения функций
.
Похожие вопросы
Предмет: Русский язык,
автор: routet
Предмет: Русский язык,
автор: анютик105
Предмет: Английский язык,
автор: volkova531514
Предмет: Математика,
автор: 7eshubina
Предмет: Французский язык,
автор: АринаФедосова
y=(x³+4)(x²-3)
y=x⁵-3x³+4x²-12
y'=5x⁴-9x²+8x
2)
y=√(x)*(4x-3)
y=x^(1/2)*(4x-3)
y=4x^(3/2)-3x^(1/2)
y'=6x^(1/2)-3/2x^(-1/2)
y'=6√(x)-3/(2√x)
3)
y=(√(x)-2)*(5-6√(x))
y=5√(x)-6x-10+12√(x)
y'=5/(2√x)-6+6/√(x)