Question

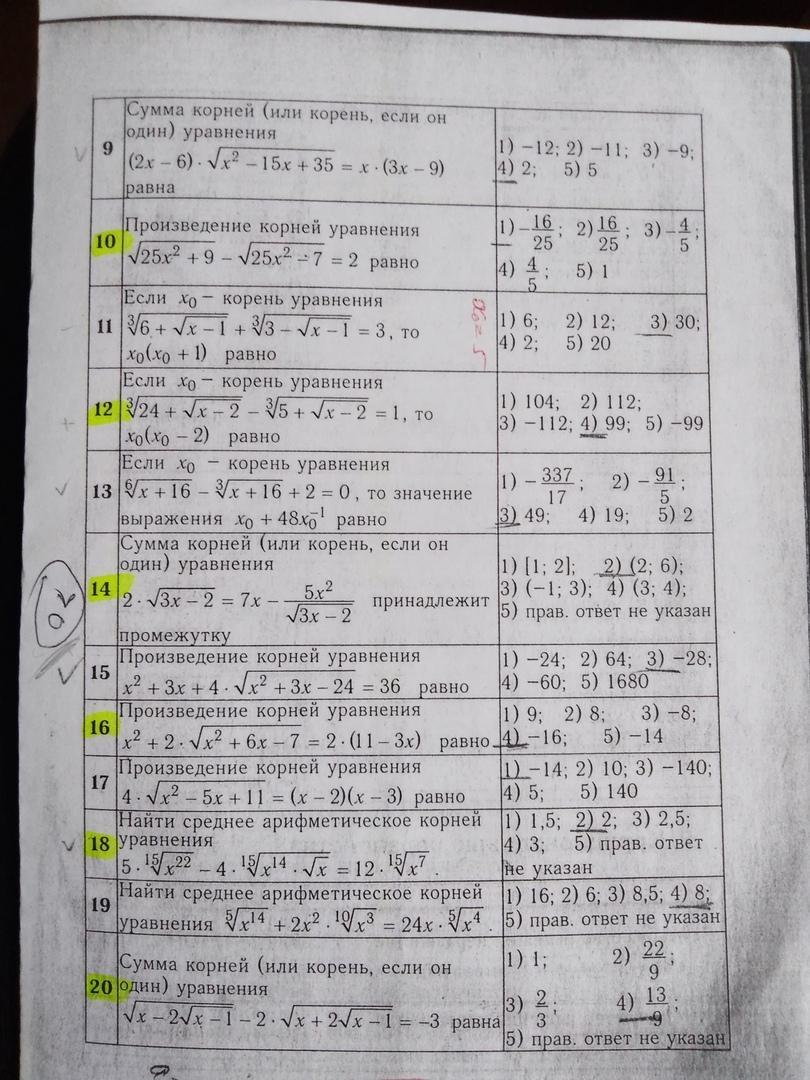
Помогите решить ЦТ (нужно решить 12.14.16)

Answer 1

14.

Возводим обе части уравнения в куб:

$24+\sqrt{x-2} -3\sqrt[3]{24+\sqrt{x-2} } \cdot \sqrt[3]{5+\sqrt{x-2} }\cdot (\sqrt[3]{24+\sqrt{x-2} } - \sqrt[3]{5+\sqrt{x-2} })-5-\sqrt{x-2}=1$

Так как выражение в скобках равно 1

$24+\sqrt{x-2} -3\sqrt[3]{24+\sqrt{x-2} } \cdot \sqrt[3]{5+\sqrt{x-2} }-5-\sqrt{x-2}=1$

$\sqrt[3]{24+\sqrt{x-2} } \cdot \sqrt[3]{5+\sqrt{x-2} }=6$

Возводим в куб:

$(24+\sqrt{x-2} ) \cdot (5+\sqrt{x-2})=216$

Замена переменной:

$\sqrt{x-2}=t$

$(24+t) \cdot (5+t)=216$

Квадратное уравнение:

$t^2+29t-96=0$

$D=29^2+4\cdot 96=841+384=1225$

$t_{1}=\frac{-29-35}{2}$   или $t_{2}=\frac{-29+35}{2}$

$t_{1}=-32$   или $t_{2}=3$

$\sqrt{x-2}=-32$   или $\sqrt{x-2}=3$

не имеет корней   или      $x-2=9$    ⇒   $x=11$

$x_{o}=11$

$x_{o}(x_{o}-2)=11\cdot (11-2)=11\cdot 9=99$

О т в е т. 99

14.

$2\sqrt{3x-2} =7x-\frac{5x^2}{\sqrt{3x-2} }$

Замена переменной:

$\sqrt{3x-2}=t$

$2t=7x-\frac{5x^2}{t}$

$t\neq 0$

$2t^2-7xt+5x^2=0$

$D=(-7x)^2-4\cdot 2\cdot 5x^2=49x^2-40x^2=9x^2$

$t_{1}=\frac{7x-3x}{4}$   или $t_{2}=\frac{7x+3x}{4}$

$t_{1}=x$      или     $t_{2}=\frac{5}{2}x$

$\sqrt{3x-2}=x$   или   $\sqrt{3x-2}=\frac{5}{2}x$

возводим в квадрат

$3x-2=x^2$         или       $3x-2=\frac{25}{4}x^2$

$x^2-3x+2=0$        или      $25x^2-12x+8=0$  нет корней   D <0

по теореме Виета

сумма корней равна 3

О т в е т. 3 ∈ (2;6)

16.

$x^2+2\sqrt{x^2+6x-7} =2\cdot (11-3x)$

$x^2+6x-22+2\sqrt{x^2+6x-7} =0$

Замена переменной:

$\sqrt{x^2+6x-7} =t$

$x^2+6x-7 =t^2\\\\x^2+6x=t^2+7$

$t^2+7-22+2t=0\\\\t^2+2t-15=0$

$D=4+60=64$

$t_{1}=-5$   или $t_{2}=3$

$\sqrt{x^2+6x-7} =-5$   не имеет корней

$\sqrt{x^2+6x-7} =3$   возводим в квадрат       $x^2+6x-7 =9$

$x^2+6x-16 =0$

по теореме Виета произведение корней равно    $-16$