Question

Основания равнобедренной трапеции равны 10 и 24, а ее периметр равен 84. Найдите площадь трапеции.

Answer 1

Допустим,что трапеция это ABCD

BH-высота трапеции

ABH-прямоугольный треугольник

1)AB=84-(10+24)/2=25 см

2)AH=24-10/2=7 см

3)BH^2=AB^2-AH^2=25^2-7^2=576

BH=под корнем 576=24 см

Мы нашли высоту трапеции

4)Площадь трапеции вычисляется по формуле:S=a+b/2 *h

S=10+24/2×24=408

Answer 2

Ответ:  S  = 408 ед²

Пошаговое объяснение:

Раз трапеция равнобедренная , то ее боковые стороны равны , а периметр равен сумме боковых сторон и двух оснований .
( x - длина боковой стороны трапеции )

P = 10+24 + x + x = 84

2x = 84-34

x = 25  

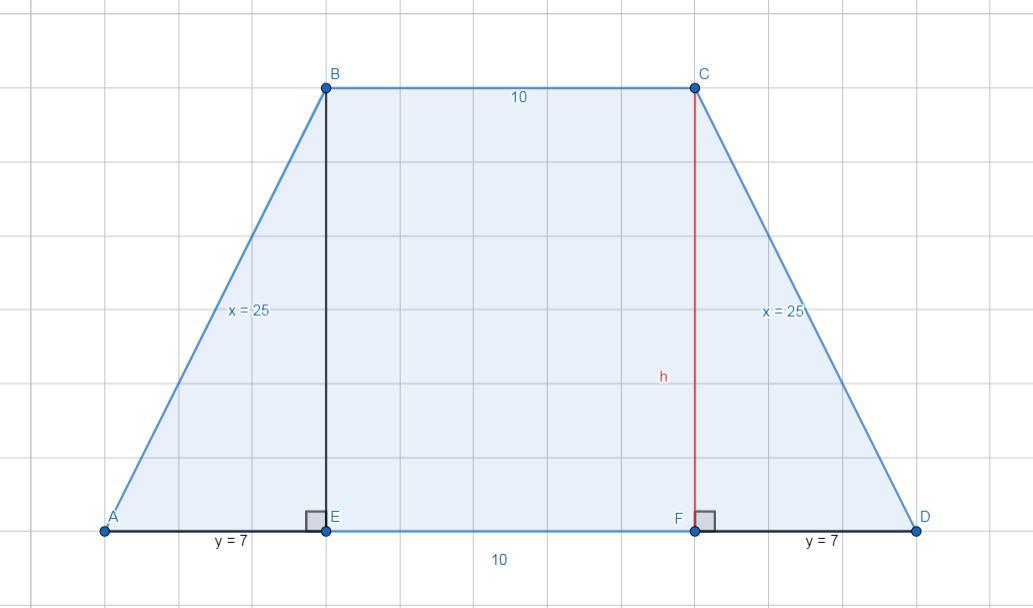
На основание AC опустим высоту  CF

Так как трапеция равнобедренная то AE = FD = y  

И также мы знаем что

AE+EF+FD = AD

2y+10 = 24

y = 7  

Высоту  CF = h  можно  найти по теореме Пифагора

h² + y² = x²

h² = x² - y²

$h =\sqrt{x^2- y^2} =\sqrt{25^2- 7^2} =\sqrt{576} = 24$

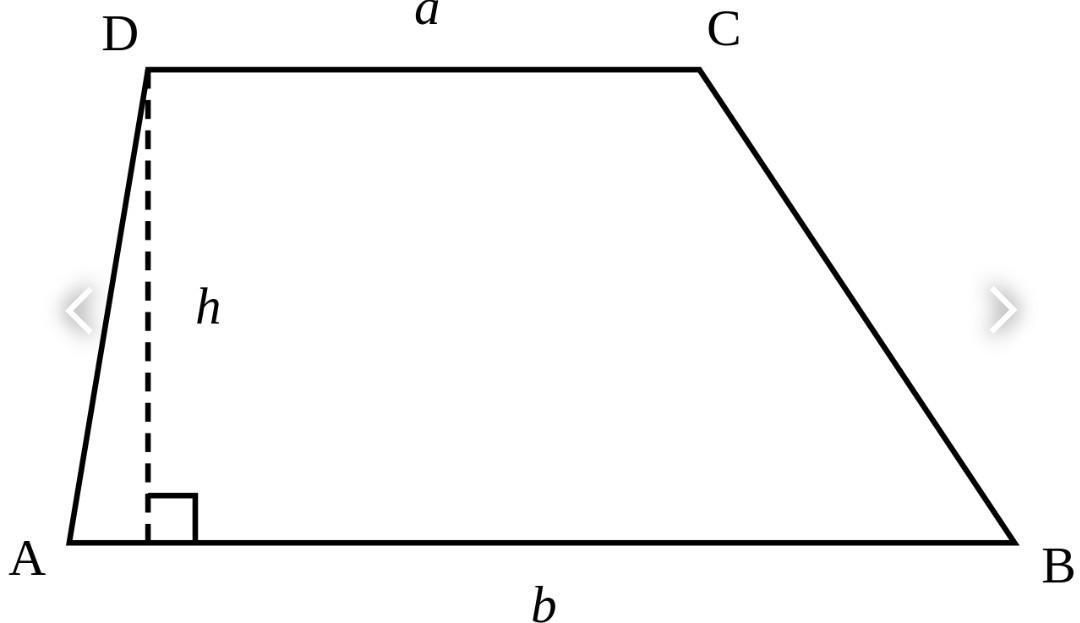
Площадь трапеции вычисляется формулой :

$S =\dfrac{a+b}{2} \cdot h$

где a,b - основания трапеции ; а h - высота

Тогда

$S =\dfrac{10+24}{2} \cdot 24 = 17 \cdot 24=408$