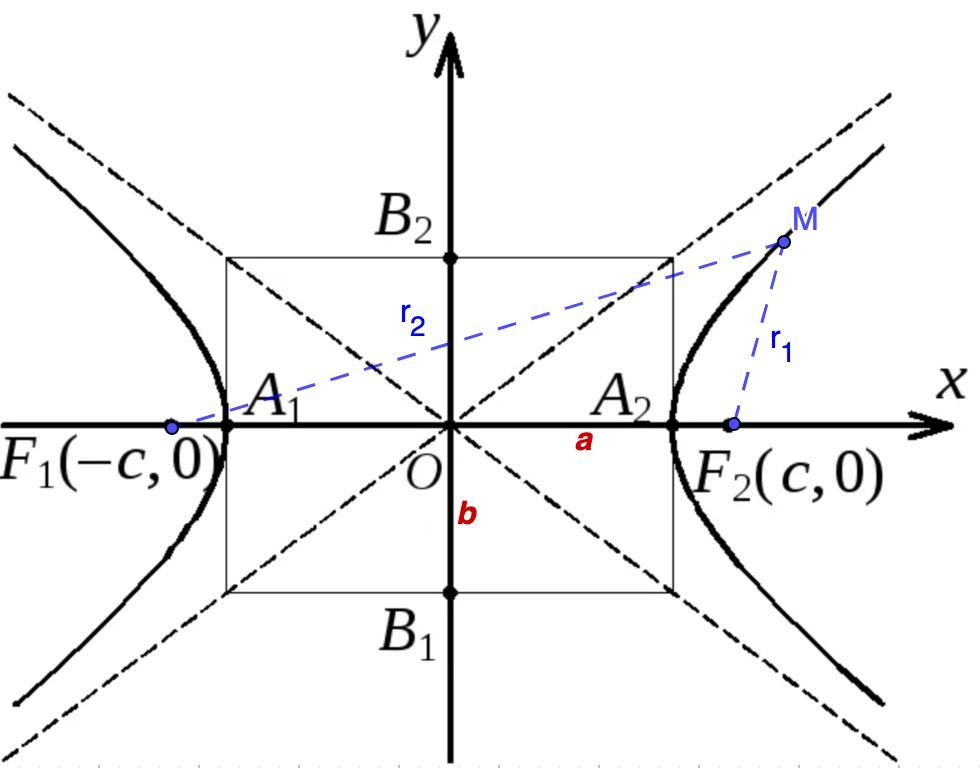
Знайти осі вершини фокуси ексцентриситет та рівняння асимптот гіпербрли 4x²-5y²-100=0
Ответы
Ответ:
1. Вершины гиперболы А₁(-5; 0); А₂(5;0);
2. Оси:
AA₁= 10 - действительная ось гиперболы.
BB₁ = 4√5 - мнимая ось гиперболы.
3. Фокусы F₁(-3√5; 0), F₂(3√5; 0);
4. Эксцентриситет гиперболы: ;
5. Асимптоты:
Пошаговое объяснение:
Требуется знайти осі, вершини, фокуси, ексцентриситет та рівняння асимптот гіпербрли 4x²-5y²-100=0.
- Гипербола - множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, причем это постоянная меньше расстояния между фокусами.
Каноническое уравнение гиперболы имеет вид:
1. Приведем данное уравнение гиперболы к каноническому виду. Для этого (-100) перенесем вправо. Затем разделим на 100 обе части уравнения:
то есть а = 5; b = 2√5.
2. Точки А₁(-а; 0) и А₂(а; 0) - вершины гиперболы.
⇒ А₁(-5; 0); А₂(5;0)
3. AA₁ = 2a = 10 - действительная ось гиперболы.
BB₁ = 2b = 4√5 - мнимая ось гиперболы.
4. Фокусы гиперболы имеют координаты F₁(-c; 0), F₂(c; 0)
c² = a² + b²
c² = 25 + 20 = 45
c = √45 = 3√5
⇒ F₁(-3√5; 0), F₂(3√5; 0)
5. Эксцентриситет гиперболы:
6. Гипербола имеет две асимптоты: