Question

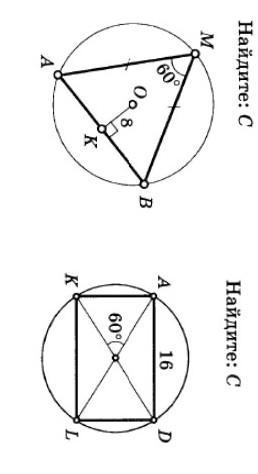
C-длина окружности, в обоих задачах надо найти С. ДАЮ 40 БАЛЛОВ!!!​

Answer 1

$\pi$Ответ:

№1:

1) Медиана проходит через центр равностороннего треугольника с отношением 2:1, то-есть 2:1=MO:KO => MO=2KO=16

2) тк O-центр окружности и M принадлежит кругу, ОМ-радиус окружности

3) по формуле C=2$\pi$R, найдем C=2$\pi$MO=2*$\pi$*16=32$\pi$

№2:

1) рассмотрим треугольник AOK где О-середина окружности; по св-вам прямоугольника треугольник АOK-равнобедренный значит, что углы KAO и OKA равны => уг.KAO=уг.OKA=(180-уг.AOK)/2=(180-60)/2=120/2=60 =>углы KAO, OKA и AOK равны, следовательно треугольник AOK-равносторонний

2) рассмотрим прямоугольный треугольник KAD; уг. DAK=60, уг. KAD=90, уг. ADK=180-KAD-DAK=180-60-90=30.

3) По теореме Пифагора, AD=KA$\sqrt{3}$ => KA=AD/$\sqrt{3}$=$\frac{16}{\sqrt{3} }$

4) KA=AO, где AO - радиус окружности

5) C=2$\pi$R, найдем С=2$\pi$AO=2*$\pi$*$\frac{16}{\sqrt{3} }$=$\frac{32\pi }{\sqrt{3} }$

Объяснение: