Предмет: Алгебра,
автор: Аноним
помогите!!!!!!!!!!!!!!!!!умоляю!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:

Ответы
Автор ответа:
0
Решение смотри во вложениях
Приложения:

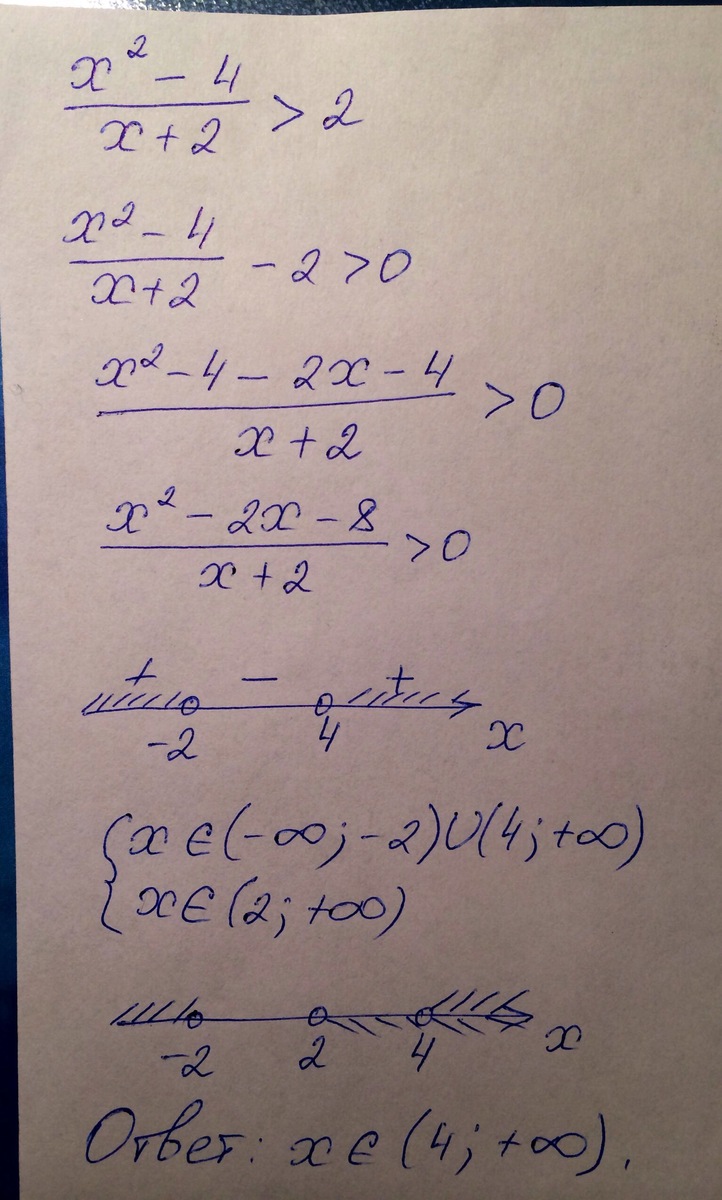
Автор ответа:
0
де е=2,71821828... основа натурального логарифма
обидва значення х входять в область визначення, тому х=-2, х=1;
визначемо облать визначення, як і в попередньому завданні, підлогарифмічний вираз має бути більше 0;
<2;><2;\>тобто Відповідь:-2<x<2 або х∈(-2;2);
Оскільки основа логарифму 0<1/2<1, то підлогарифмічні функції матимуть протилежний знак, ніж сама нерівність логарифмів
бо при потенціюванні,
розв'яжемо нерівність:
Відповідь: 2<x<4 => x∈(2;4).
Приложения:

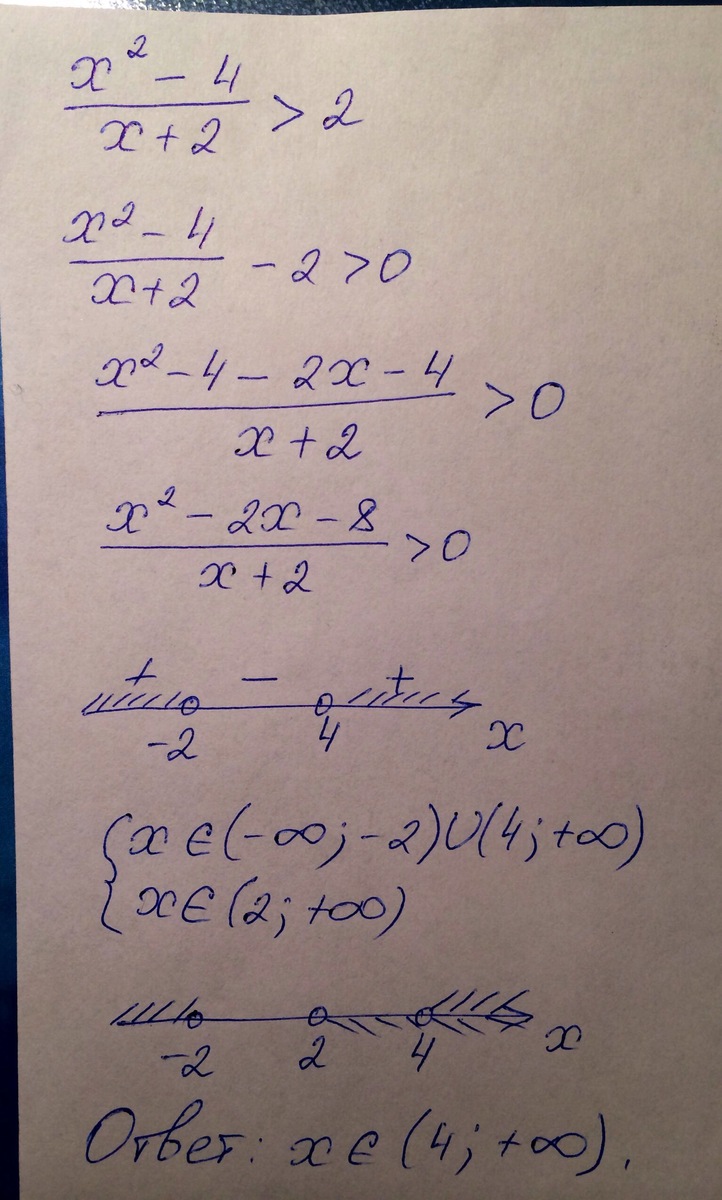
Автор ответа:
0
А вот в ручную их можно случайно добавить.
Автор ответа:
0
я уже призабіл латех, а тут панель инструментов не очень полная
Автор ответа:
0
Там ещё и окошко маленькое.
Автор ответа:
0
браво
Автор ответа:
0
Это я про окошко редактирования формул, если что... Оно маленькое и неудобное.
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: gajdarov04
Предмет: Информатика,
автор: cool338