Предмет: Алгебра,
автор: alexpol7991
Даю 50 балов помогите срочно!!!
Приложения:
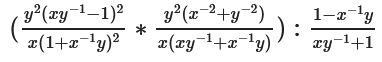
Ответы
Автор ответа:
1
Упростим каждую дробь:
Тогда
Похожие вопросы
Предмет: Английский язык,
автор: джени95
Предмет: Русский язык,
автор: Liza451083
Предмет: Русский язык,
автор: bewzo
Предмет: Биология,
автор: evgeniamelnikova90