Предмет: Математика,
автор: 29dima11
В треугольник, длины сторон которого относятся как m : n : p, вписан
круг. Найти отношение, в котором каждая точка касания делит
соответствующую сторону треугольника.
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Задание: В треугольник, длины сторон которого относятся как m : n : p, вписан круг.
Найти отношение, в котором каждая точка касания делит
соответствующую сторону треугольника.
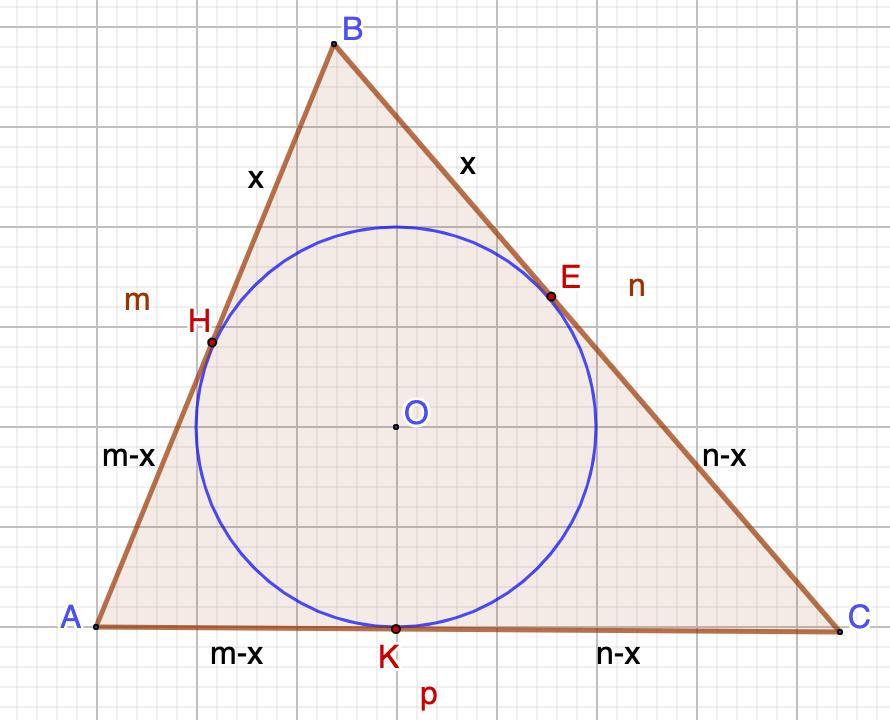
Дано: Окр.О - вписана в ΔАВС.
АВ : ВС : АС = m : n : p
Найти: ВН : НА; ВЕ : ЕС; АК : КС.
Решение:
- Отрезки касательных к окружности, проведенные из одной точки, равны.
Примем НВ = х.
Тогда, согласно теореме о касательных:
ВЕ = х.
АН = m - x ⇒ AK = m-x
EC = n - x ⇒ KC = n - x
С другой стороны:
КС = р - АК = р - (m-x)
Отрезки выразили. Но надо избавиться от х.
Составим уравнение и выразим х:
p - (m - x) = n - x
p - m + x = n - x
2x = n + m - p
Подставим вместо х его значение в выше написанные равенства:
Найдем искомые отношения:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: мила0055
Предмет: Другие предметы,
автор: olgalubnina201
Предмет: Қазақ тiлi,
автор: Helper830
Предмет: Химия,
автор: HNLLZ
Предмет: Английский язык,
автор: Аноним