Предмет: Математика,
автор: Аноним
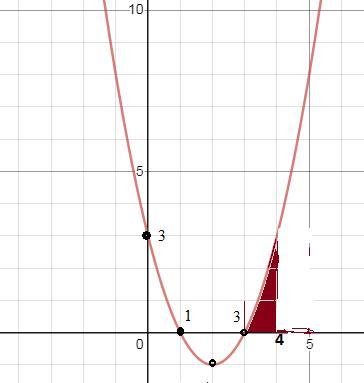
Вычислите площадь фигуры, ограниченной линиями
y=x^2-4x+3, y=0, x=3 и x=4
СПАСИБО ЗА ПОМОЩЬ!!! По теме интегралы и его применение
Ответы
Автор ответа:
1
Ответ: 4/3 (кв.ед)
Пошаговое объяснение:
1)Построим схематично график функции у=х²-4х+3 ;
для этого найдём абсциссы точек пересечения с осью ОХ:
х²-4х+3=0
D=16-12=4 ⇒ x₁=1; х₂=3
Парабола направлена ветвями вверх, т.к. а=1>0
2) ограничим параболу линиями y=0, x=3 и x=4
3) закрасим полученную область.
4)Площадь полученной фигуры равна:
S =∫₃⁴(х²-4х+3)dx = (x³/3 -2x²+3x) |₃⁴ = 64/3 - 32+12 - (27/3 -18+9)= 64/3 -32+12-9+18-9= 64/3 -20 = 64/3 - 60/3 = 4/3 (кв.ед)
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: мээрим01
Предмет: Русский язык,
автор: Pechenka100500
Предмет: Русский язык,
автор: АняАнгел
Предмет: Английский язык,
автор: nemo1319
Предмет: Математика,
автор: danilshirin2008