Предмет: Алгебра,
автор: TheUbay
Помогите с примером пожалуйста, отдаю все баллы
Приложения:
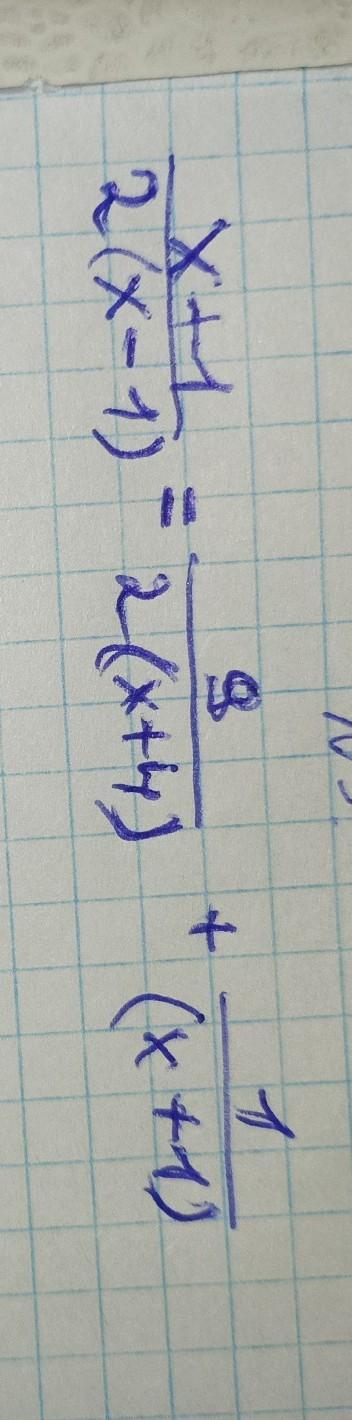
TheUbay:
Решить
Упростить? Или это уравнение? Получается многочлен в решении. Может, многочлен в стандартном виде записать?
???
Задание за какой класс ?
8 класс
Тогда в вопросе 100% опечатка
Скажите об этом учителю
Выходит кубическое уравнение , которое нельзя решить методом группировки .
ок , спасибо большое за помощь.
Согласна)
Ответы
Автор ответа:
3
Ответ: x₁ = 1,4 и x₂ = -1,5
Объяснение:
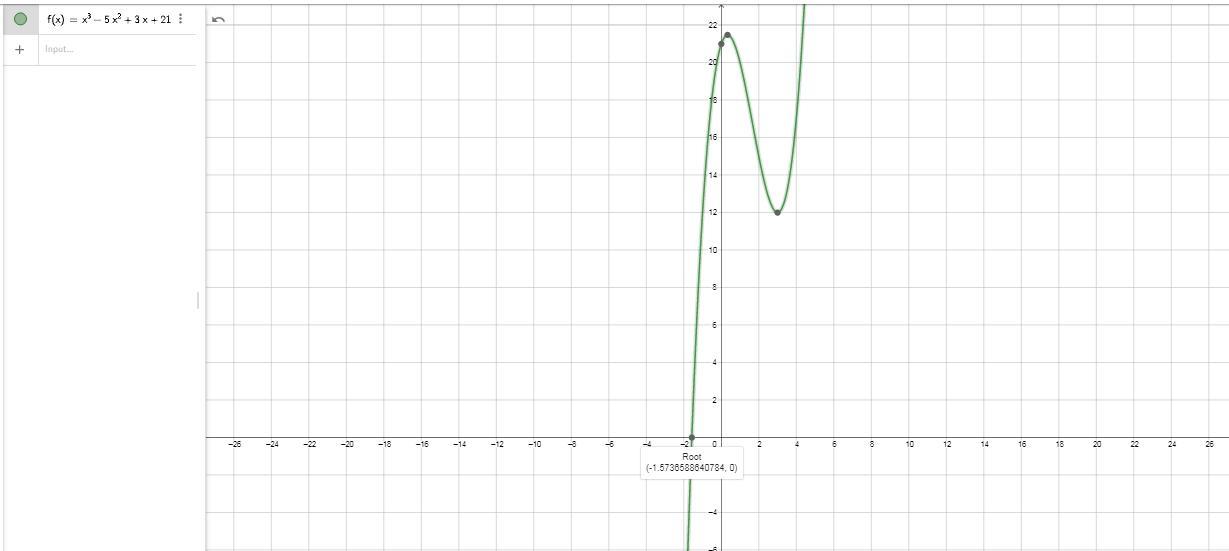
По графику видно что решение находится в точке (-1,5736 ; 0 )
Со слов автора вопроса : задача за 8 класс , тогда в вопросе опечатка и оно должно было быть таким :
Различие уже в том что выходит квадратное уравнение
Оба корня подходят по ОДЗ
Приложения:
В первой строчке решения (х + 1)^2 * (х + 4), извините)
Да я заметил , сейчас исправлю
спасибо
Так что с решением? Уравнение не вышло? Я тоже зависла) При том, что задания нет.
там было написано , "решите уравнение"
Да не вышло , там скорее всего как у меня уравнение должно быть .
это правильный ответ, как я понял?
Да все совпало как ни странно , и дискриминант красивый , и числа .
Еще раз спасибо за ответ
Пожалуйста , сам недавно решал похожую задачу за 8 класс , там был похожий случай ( там выходило куб. уравнение ) , но только я так и не смог найти правильное условие , да и учитель сказал оставить .
Похожие вопросы
Предмет: Английский язык,
автор: Настя9474
Предмет: Английский язык,
автор: Сергей25200011
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: seruhckov
Предмет: Математика,
автор: Raana66