Question

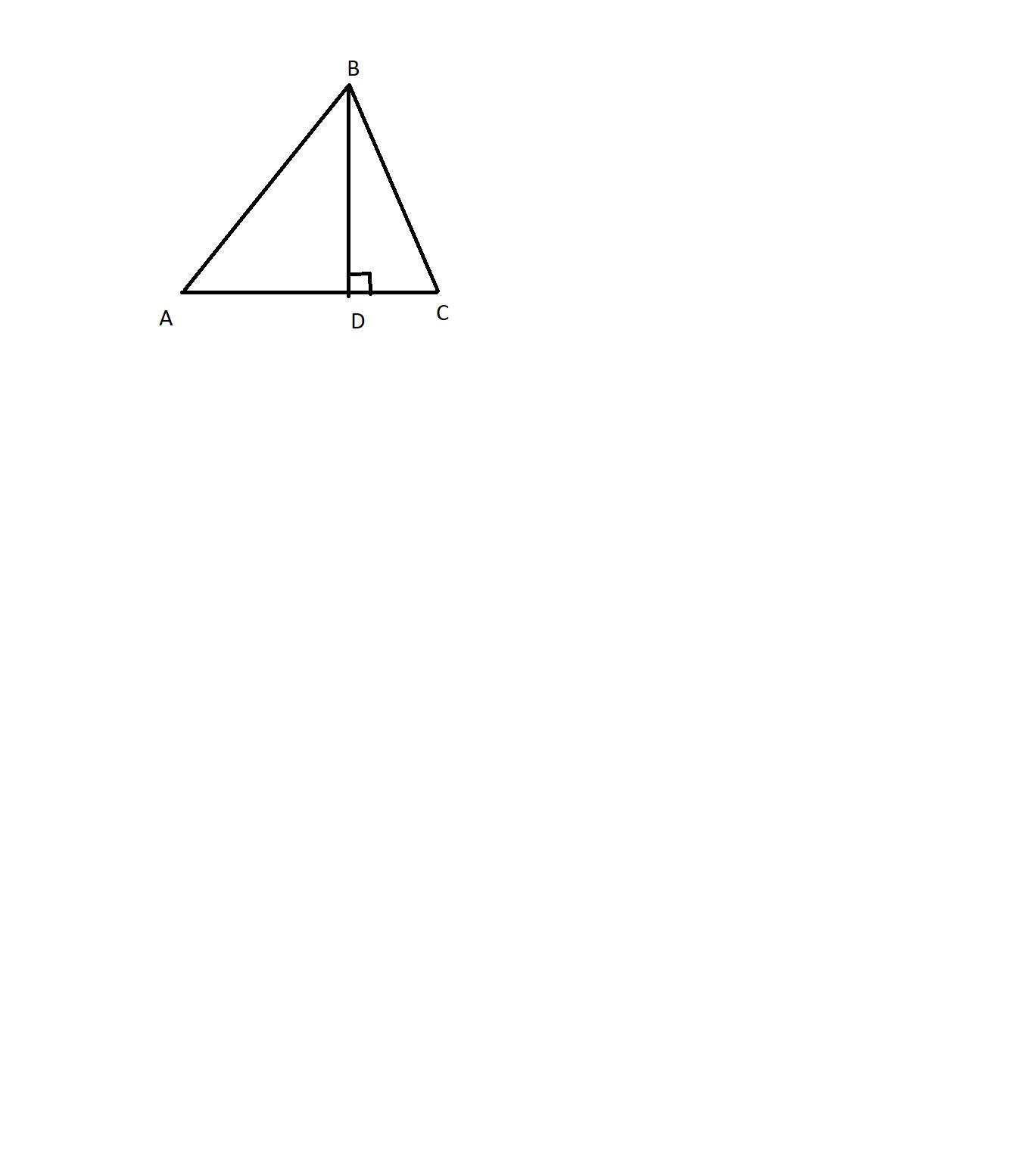
В трикутнику АВС бічна сторона ВС утворює з основою АС кут 30 градусів, а висота опущена з вершини В ділить основу на відрізки АД=12, ДС=5 квадратний корінь з 3 см. Знайдіть бічні сторони трикутника.



Пожалуйста!!! Можно на украинском языке и с объяснением!!!​

Answer 1

Кут ABC = a = 30 градусів; AD = 12см; DC = 5$\sqrt{3}$см;

Розглянемо трикутник BCD: кут D = 90градусів. трикутник BCD - прямокутний, тому можна застосувати косинус для пошуку гіпотенузи.

cos a = DC/BC = $\sqrt{3}$/2; кос 30 градусів = $\sqrt{3}$/2;

ВС = DC/cos a = DC*2/$\sqrt{3}$ = 2*5$\sqrt{3}$/$\sqrt{3}$ = 10см.

Тепер знайдемо висоту BD з цього ж трикутника за тангенсом кута.

tg a = BD/DC = $\sqrt{3}$/3; звідси: BD= DC*tg a = 5$\sqrt{3}$ *$\sqrt{3}$/3 = 5 см.

Розглянемо трикутник АBD: кут D =90 градусів. Трикутник прямокутний. AB - гіпотенуза. За т.Пфігора: AB^2 = BD^2 + AD^2 = 25+144 = 169 см^2; AB = 13 cм.

Відповідь: ВС = 10см; AB = 13 cм.