Question

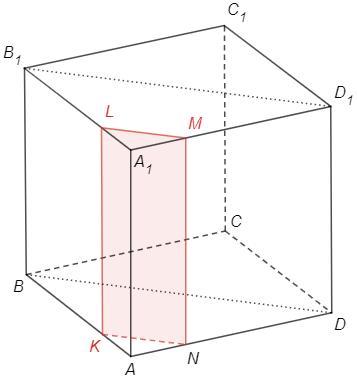
Дано куб АВСDА1В1С1D1. Точка N ділить ребро АD у відношенні АN:ND = 3:8. Побудувати переріз куба площиною, яка проходить через точку N і паралельна площині BDD1. Знайти периметр побудованого перерізу, якщо ребро куба дорівнює 22 см.

Answer 1

Ответ:

S(KLMN) =132√2 (см^2)   ~186,68

Объяснение:

Плоскость сечения параллельна диагональной плоскости BB1D1D.

Следы сечения в гранях параллельны диагоналям и боковым ребрам.

KN||LM||BD, KL||NM||BB1

Cечение - прямоугольник.

Одна сторона равна ребру, KL=BB1=22.

Другую найдем из подобия треугольников AKN и ABD (стороны параллельны).

BD =AB√2 =22√2 (диагональ квадрата)

KN/BD =AN/AD =3/11 => KN =22√2 *3/11 =6√2

S(KLMN) =22*6√2 =132√2 (см^2)