Предмет: Математика,
автор: emem83
Помогите, пожалуйста!
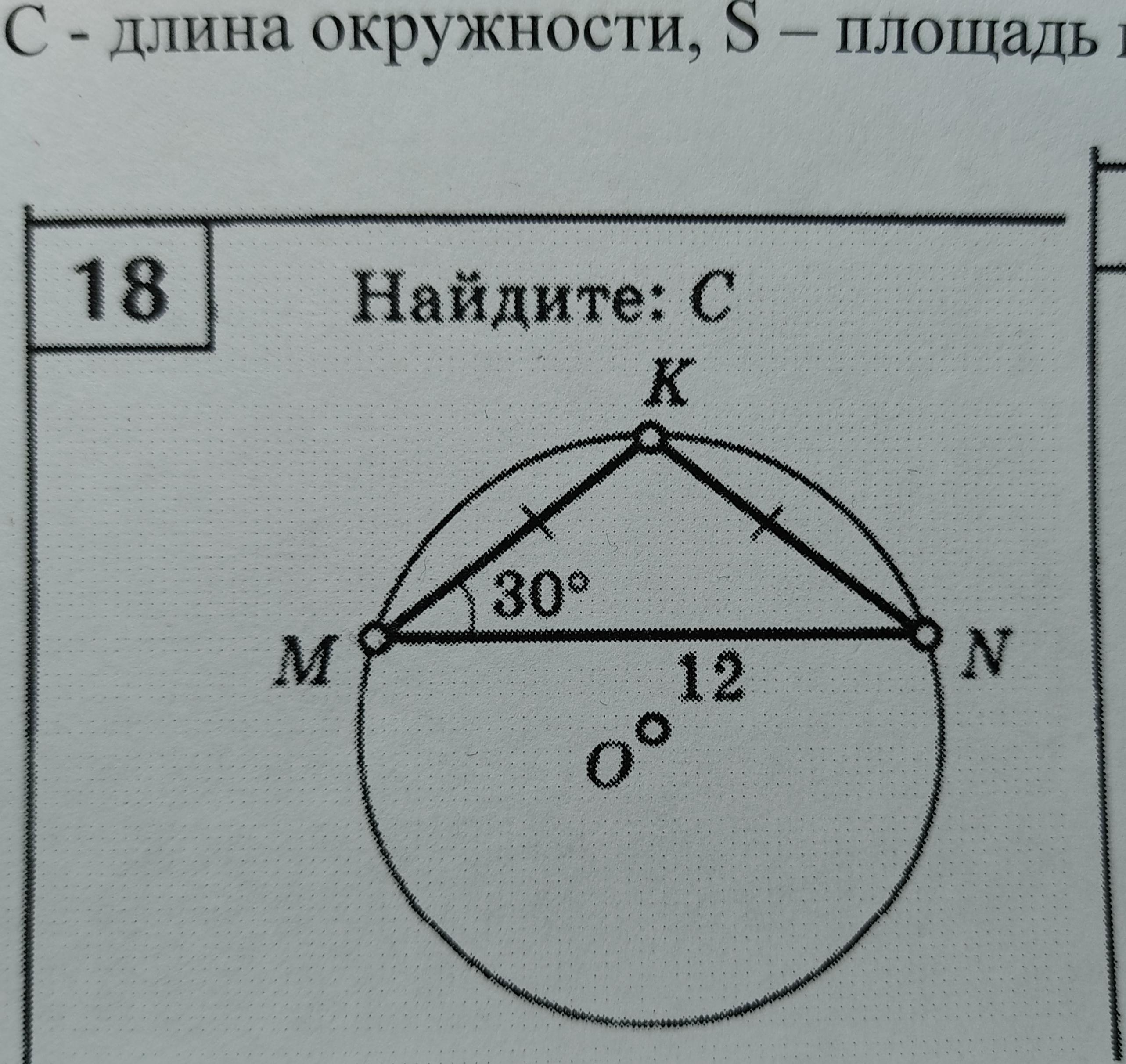
Дан треугольник MKN. Угол KMN=30°, MN=12. Найдите: C
Приложения:
Ответы
Автор ответа:
0
Чтобы найти длину окружности, надо знать ее радиус, поскольку
с =2πR,
т.к. ∠М=∠N=30°, что следует из того, что ΔКМN- равнобедренный, значит, ∠К=180°-2*30°=120°, а по следствию из теоремы синусов,
МN/sin∠К=2R⇒2R=12/sin120°=12/sin60°=12/(√3/2)=8√3, значит, с=8π√3
Автор ответа:
0
Ответ:
8π√3
Пошаговое объяснение:
1) т.к. треугольник KMN — равнобедренный, значит, угол KMN = углу KNM = 30°.
2) т.к. сумма всех углов в треугольнике равна 180°, то
угол KMN + угол KNM + угол MKN = 180°
30° + 30° + угол MKN = 180°
угол MKN = 120°
3) sin MKN = sin 120° = sin (180°-60°)=sin 60°= (√3)/2
4) По теореме синусов:
MN / sin MKN = 2R
5) C = 2πR
если вам понравился мой ответ можете поставить пометку «Лучший ответ»?
Похожие вопросы
Предмет: Русский язык,
автор: Ruslan00789
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Английский язык,
автор: lltgprv
Предмет: Математика,
автор: rabbid123invasion
Предмет: Литература,
автор: NIKE126