Предмет: Алгебра,
автор: sawa0204
Решите уравнение: смотрите фото
Помогите Срочно
Приложения:
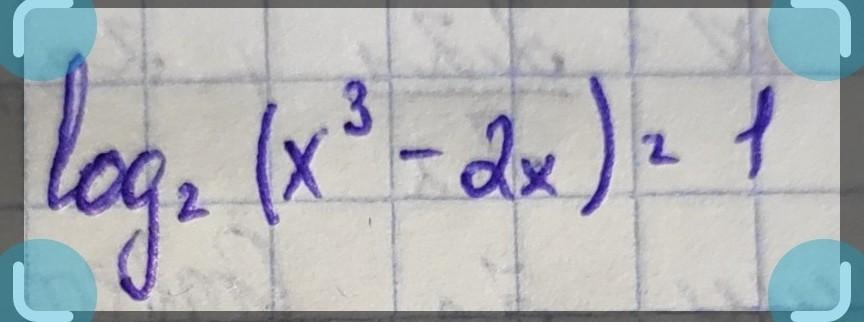
Ответы
Автор ответа:
1
Ответ:
х∈∅.
Объяснение:
ОДЗ:
Используя тот факт, что эквивалентно
преобразуем.
Воспользуемся формулой Кардано.
В нашем случае:
Подставим наши данные, посчитаем, выходит, что х=0. Но корень "х=0" не подходит по ОДЗ ⇒ корней нет.
oleksii246:
да. сейчас без ОДЗ , как без рук
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: МХК,
автор: 1qaz2wsx3edc