Question

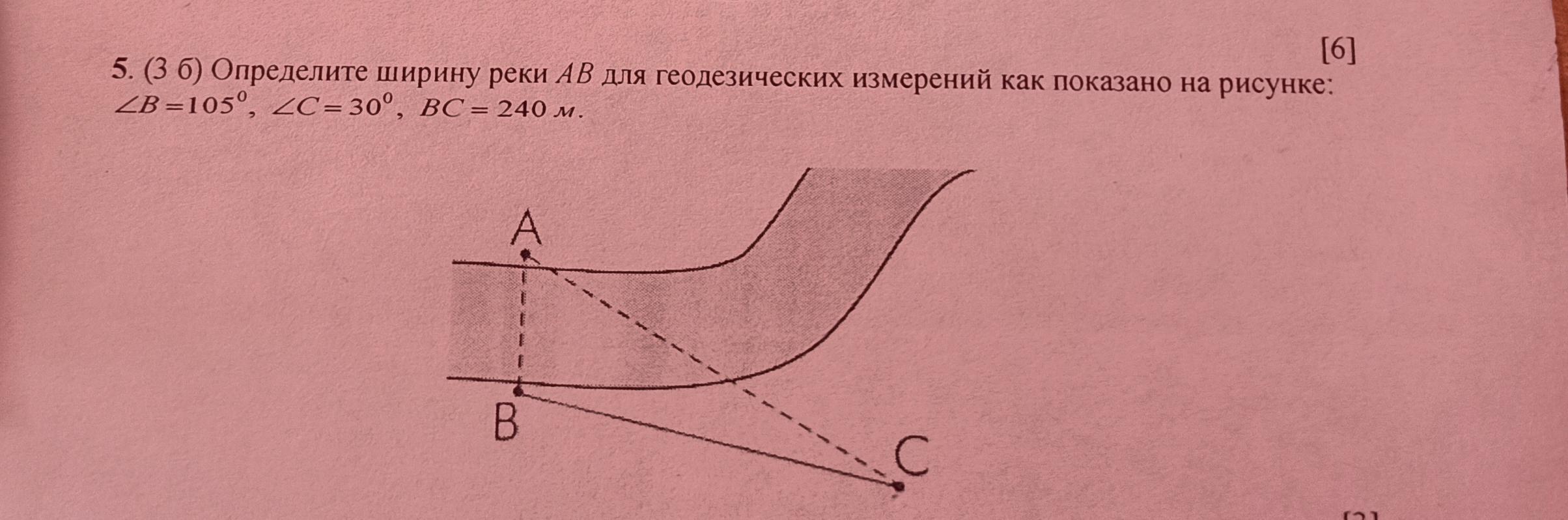
определите ширину реки AB для геодезических измерений как показано на рисунке ​

Answer 1

Ответ:  $10(\sqrt3+1)\approx 27,32$  м .

В ΔАВС :  ∠В=105°  ,  ∠С=30°  ,  ВС=240 м

Ширина реки - это отрезок АВ в тр-ке АВС .

Сумма углов треугольника = 180°, значит ∠A=180°-105°-30°=45° .

Применяем теорему синусов.

$\dfrac{AB}{sinC}=\dfrac{BC}{sinA}\ \ \ \Rightarrow \ \ \ \dfrac{AB}{sin105^\circ }=\dfrac{20}{sin45^\circ }\ \ \ ,\ \ \ AB=\dfrac{20\cdot sin105^\circ }{sin45^\circ }$  

Найдём sin105° .

$sin105^\circ =sin(60^\circ +45^\circ )=sin60^\circ \cdot cos45^\circ +cos60^\circ \cdot sin45^\circ =\\\\=\dfrac{\sqrt3}{2}\cdot \dfrac{\sqrt2}{2}+\dfrac{1}{2}\cdot \dfrac{\sqrt2}{2}=\dfrac{\sqrt2}{2}\cdot \dfrac{\sqrt3+1}{2}$

$AB=\dfrac{20\cdot \dfrac{\sqrt2}{2}\cdot \dfrac{\sqrt3+1}{2}}{\dfrac{\sqrt2}{2}}=10\cdot (\sqrt3+1)\approx 27,32$   (м)