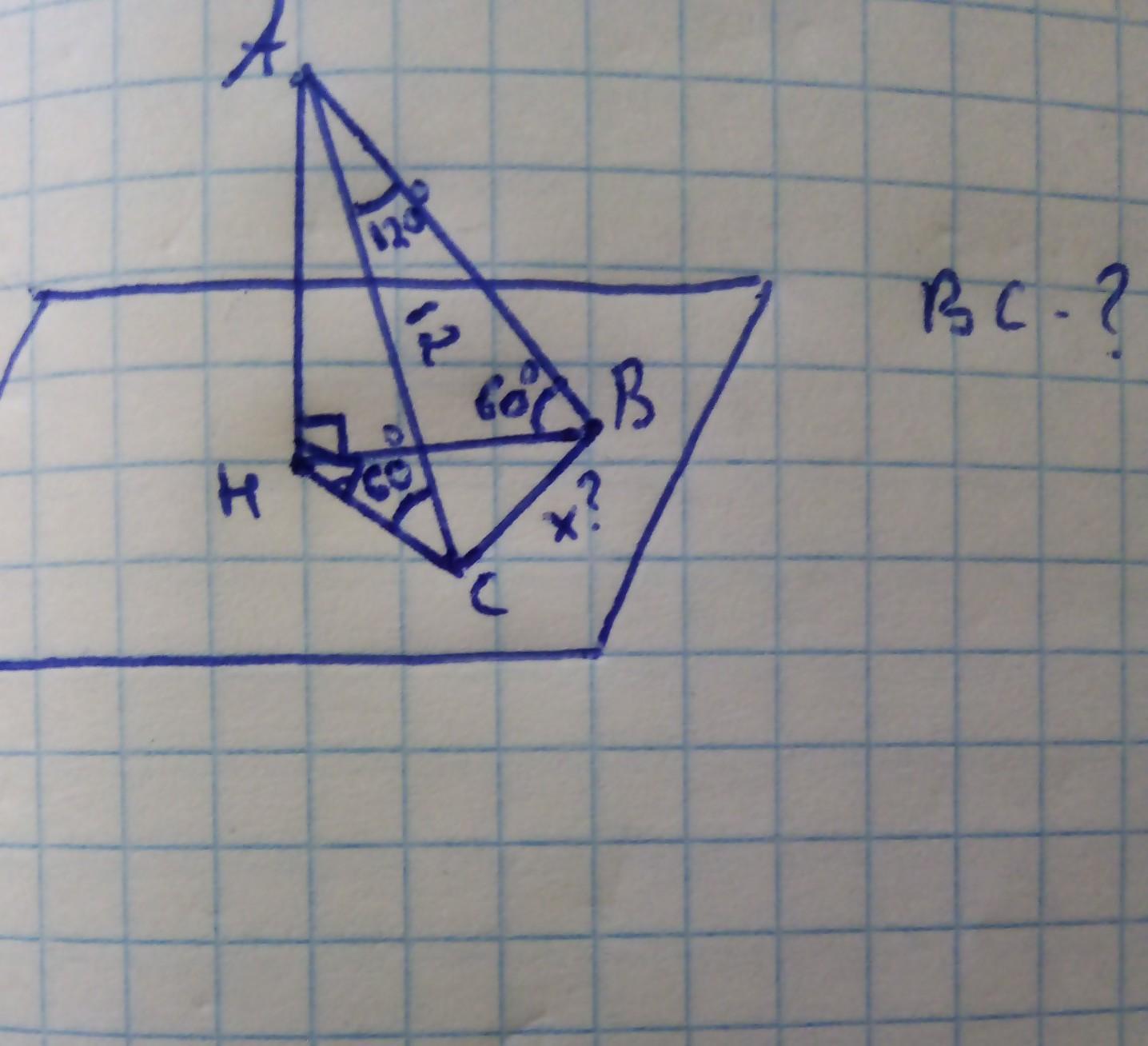
Если что она лежит на плоскости
Ответы
Ответ:
Объяснение:
1) Т.к. угол CAB=120⁰, а треугольники НАС и НАВ прямоугольные и у них углы НСА и НВА равны 60⁰, то треугольник САВ - равнобедренный и угол АСВ=АВС=(180⁰-120⁰)÷2=60⁰÷2=30⁰.
2) Если в треугольнике САВ провести высоту АН, то получится два равноправных прямоугольных треугольника (СН=НВ).
Из треугольника САН можно найти АН: т.к. уголС=30⁰, то катет лежащий напротив угла 30⁰ равен половине гипотенузы, поэтому АН=1/2×АС=1/2×12=6
по теореме Пифагора найдём СН:
12²=6²+СН²
СН²=12²-6²=144-36=108
СН= корень из 108=6корней из 3
3) ВС=2СН=2×6корней из 3=12корней из 3.
Ответ:
12√3
Объяснение:
1) т.к. АН перпендикулярно плоскости НВС, то АН перпендикулярно НС и НВ(по определению перпендикулярности прямой и плоскости) следовательно, треугольникт АВН и АСН — прямоугольные.
2) Рассмотрим треугольник АНС:
Т.к. сумма острых углов равна 90° в прямоугольном треугольнике, то угол АСН + угол САН = 90°
60°+угол САН=90°
угол САН = 30°. Аналогично, в треугольнике АВН: угол ВАН = 30°(угол АВН + угол ВАН = 90°)
3) АН — общий катет, угол СНА = углу ВАН = 30°, тогда треугольники АНС и АВН равны(по катету и прилежащему острому углу), значит, АС = АВ = 12.
4)Рассмотрим треугольник АВС:
по теореме косинусов: ВС²=АС²+АВ²-2*АВ*АС*cos САВ
х²=12²+12²-2*12*12*cos 120.
x²=2*12²-2*12*12*(-0,5)
x²=2*12²+12²
x²=3*12² → x = 12√3
если вам понравился мой ответ можете поставить пометку «Лучший ответ»?