Предмет: Алгебра,
автор: akkaowoerjrj
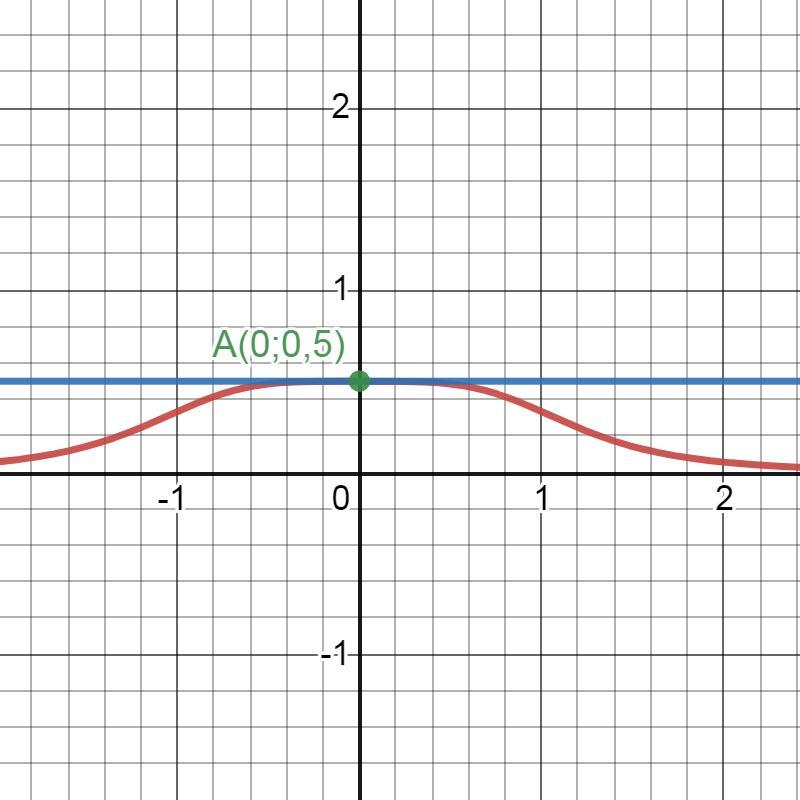
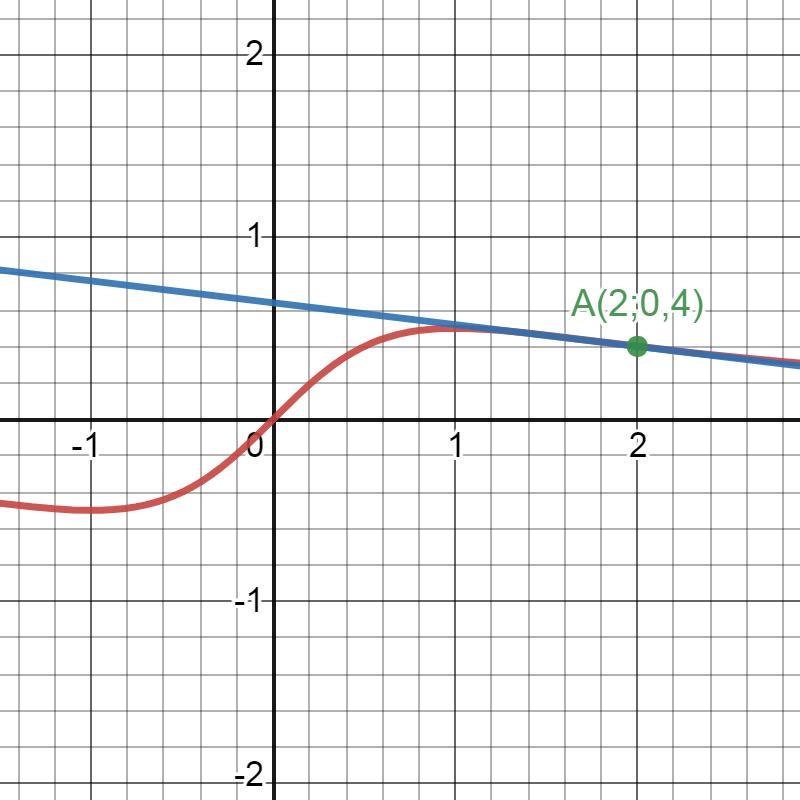
ПОМОГИТЕ ПЛИИИЗ ООЧЕНЬ СРОЧНО!!! НАПИШИТЕ УРАВНЕНИЕ КАСАТЕЛЬНОЙ К ГНАФИКУ ФУНКЦИИ y=f(x) в точке х0. Задание (2;4;6)
Приложения:
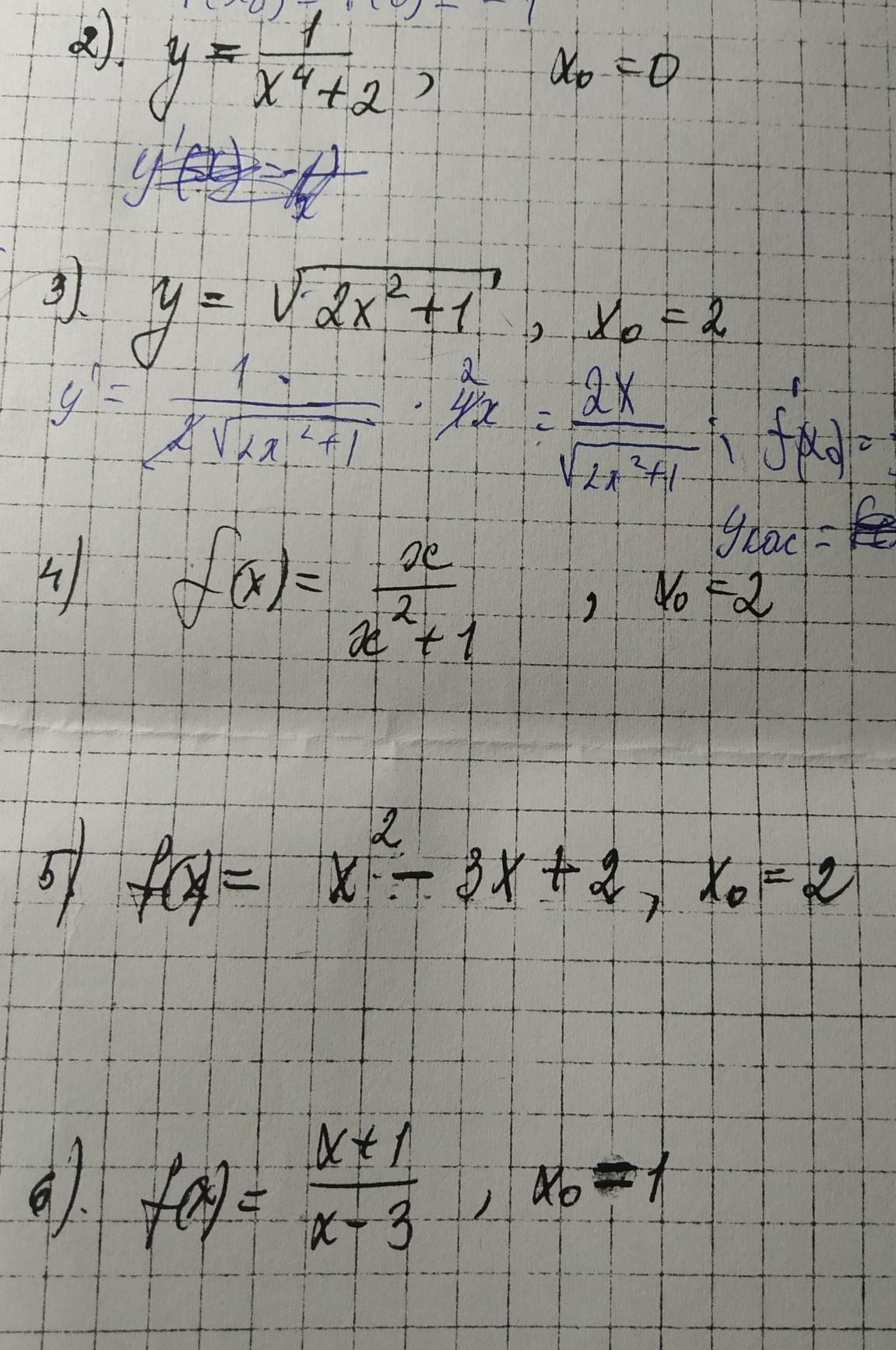
Ответы
Автор ответа:
1
Ответ:
Объяснение:
2)
Ответ: yk=0,5.
4)
Ответ: yk=-0,12x+0,64.
6)
Ответ: yk=-x.
Приложения:

akkaowoerjrj:
ЗДРАВСТВУЙТЕ СПАСИБО БОЛЬШОЕ ЗА ОТВЕТ
можете пожалуйста с последним заданием помочь у меня в профиле
он почти такой же
Похожие вопросы
Предмет: Русский язык,
автор: holiday16052004
Предмет: Русский язык,
автор: всеволод2015
Предмет: Русский язык,
автор: AleksaAxenova
Предмет: Русский язык,
автор: galymmadi2008
Предмет: Математика,
автор: kamilla6746