Сделайте пожалуйста дам 50 баллов

Ответы
Ответ:
4√3 ед.
Объяснение:
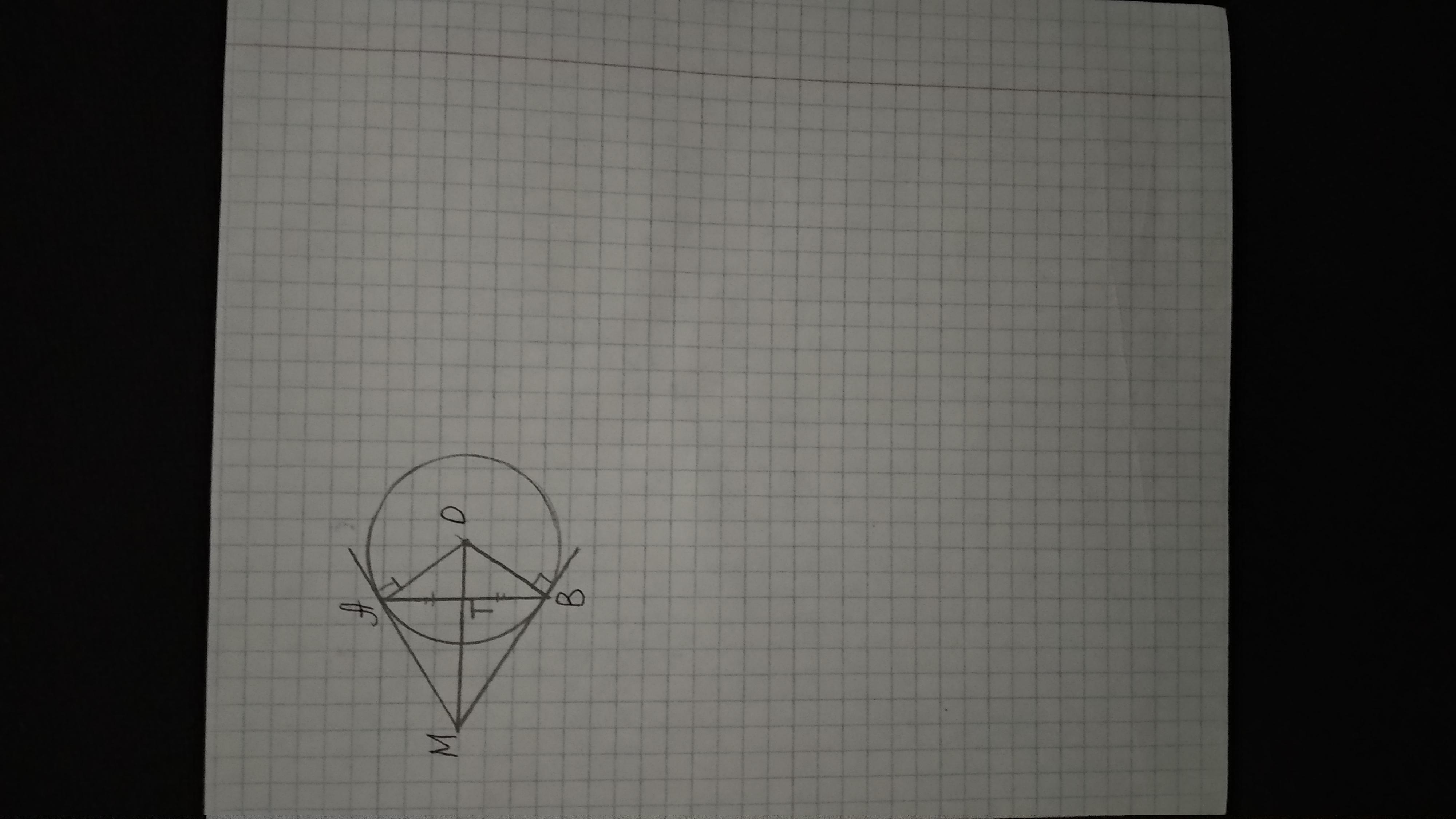
∠АОВ - равнобедренный, АО=ОВ как радиусы одной окружности
∠ОАВ=∠ОВА=(180-120):2=30°
ΔАМО - прямоугольный по свойству касательной и радиуса окружности, ∠МАО=90°
МА=МВ по свойству касательных, проведенных к окружности из одной точки
ΔМАО=ΔМВО по третьему признаку (АО=ОВ; МА=МВ; МО - общая сторона.
Тогда ∠АОМ=∠ВОМ=120:2=60°. а ∠АМО=∠ВМО=90-60=30°. По свойству катета, лежащего против угла 30°, АО=1/2 МО=4.
Найдем АВ по теореме косинусов:
АВ²=АО²+ВО²-2*АО*ВО*cos120=16+16-32*(-0,5)=32+16=48;
АВ=√48=4√3 ед.
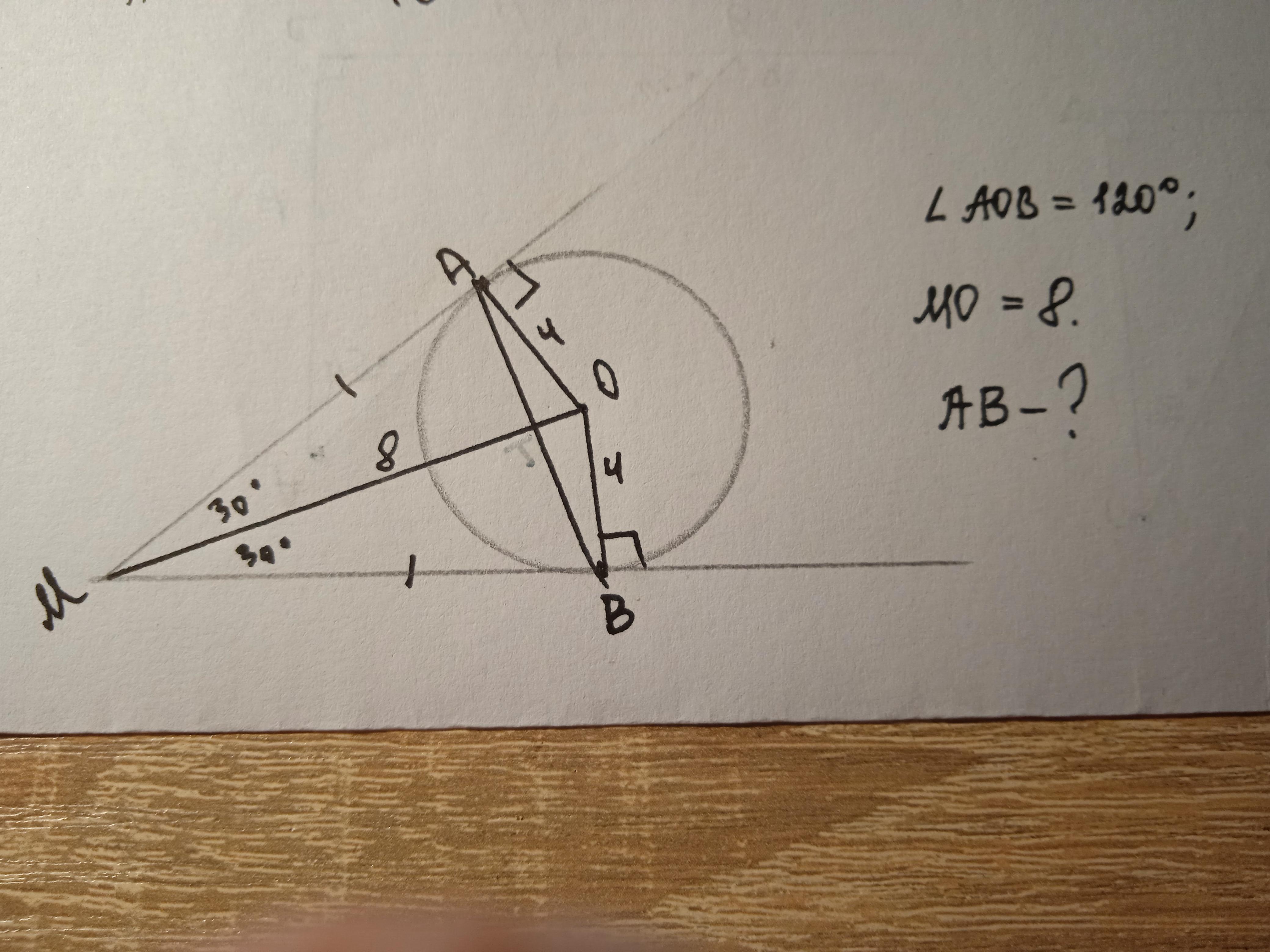
МО- биссектриса угла АОВ; в прямоугольном треугольнике АОМ ( он прямоугольный, т.к. радиус ОА , проведенный в точку касания перпендикулярен касательной МА.) радиус ОА лежит против ∠АМО=30°, т.к. ∠АОМ=120°/2=60°; ∠МАО=90°; ∠АМО=180°-90°-60°=30°; ⇒АО=4; Т,к. ОА=ОВ- как радиусы одной окружности, то
∠ОВА=∠ОАВ = (180°-120°)/2=30°, тогда МО⊥АВ, и из ΔАОВ АТ=АО*sin∠АОТ=4*sin60°=4√3/2=2√3, где Т- точка пересечения МО и АВ, а т.к. МО⊥АВ, то АО=ВО⇒ АВ=2*АТ=2*3√3=4√3
Ответ 4√3