срочно пожалуйста, помогите
Ответы
Решаю по Вашей просьбе.
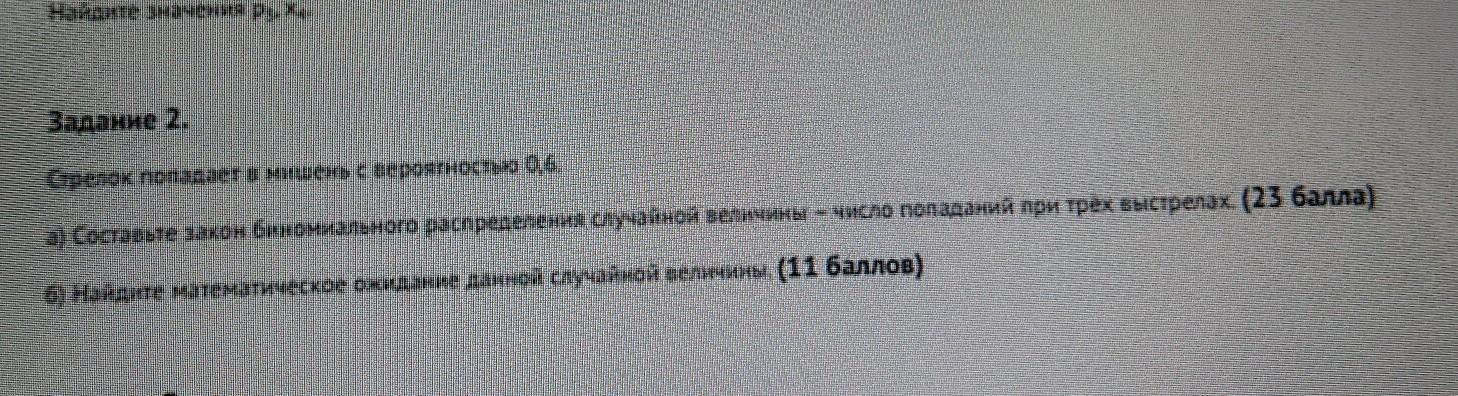
а)пусть случайная величина X -это количество
попаданий . Т.к. задан биномиальный закон распределения с параметрами р=0.6- вероятностью поразить мишень при одном выстреле, и n = 3 - числом выстрелов, которое может принимать значения от нуля до трех. ( т.е. ни попасть ни разу, один, два или все три раза)
пусть С( n, к) - это число сочетаний из n по к, оно по определению равно n!/(k!*(n-k)!), где к!=1*2*3*...к
По формуле Бернулли найдем соответствующие вероятности .
Р(Х=к)=С( n, к)*(р^k)*q^(n-к), здесь q=1-р=1-0.6=0.4- вероятность промаха при одном выстреле.
Р(Х=0)=С( 3, 0)*0.6⁰*0.4³=1*1*0.064=0.064;
Р(Х=1)=С( 3, 1)*0.6¹*0.4²=3*0.6*0.16=0.288;
Р(Х=2)=С( 3, 2)*0.6²*0.4¹=3*0.36*0.4=0.432;
Р(Х=3)=С( 3, 3)*0.6³*0.4⁰=1*0.216*1=0.216
Биномиальный закон запишем в виде таблицы.
к 0 1 2 3
________________________________________
Р(х=к) 0.064 0.288 0.432 0.216
Найдем сумму вероятностей, 0.064 +0.288 +0.432 +0.216=1 - таблица составлена правильно.
б) Математическое ожидание найдем по известной формуле для биномиального закона распределения М(Х)=n*p.
М(Х)=3*0.6=1.8