Question

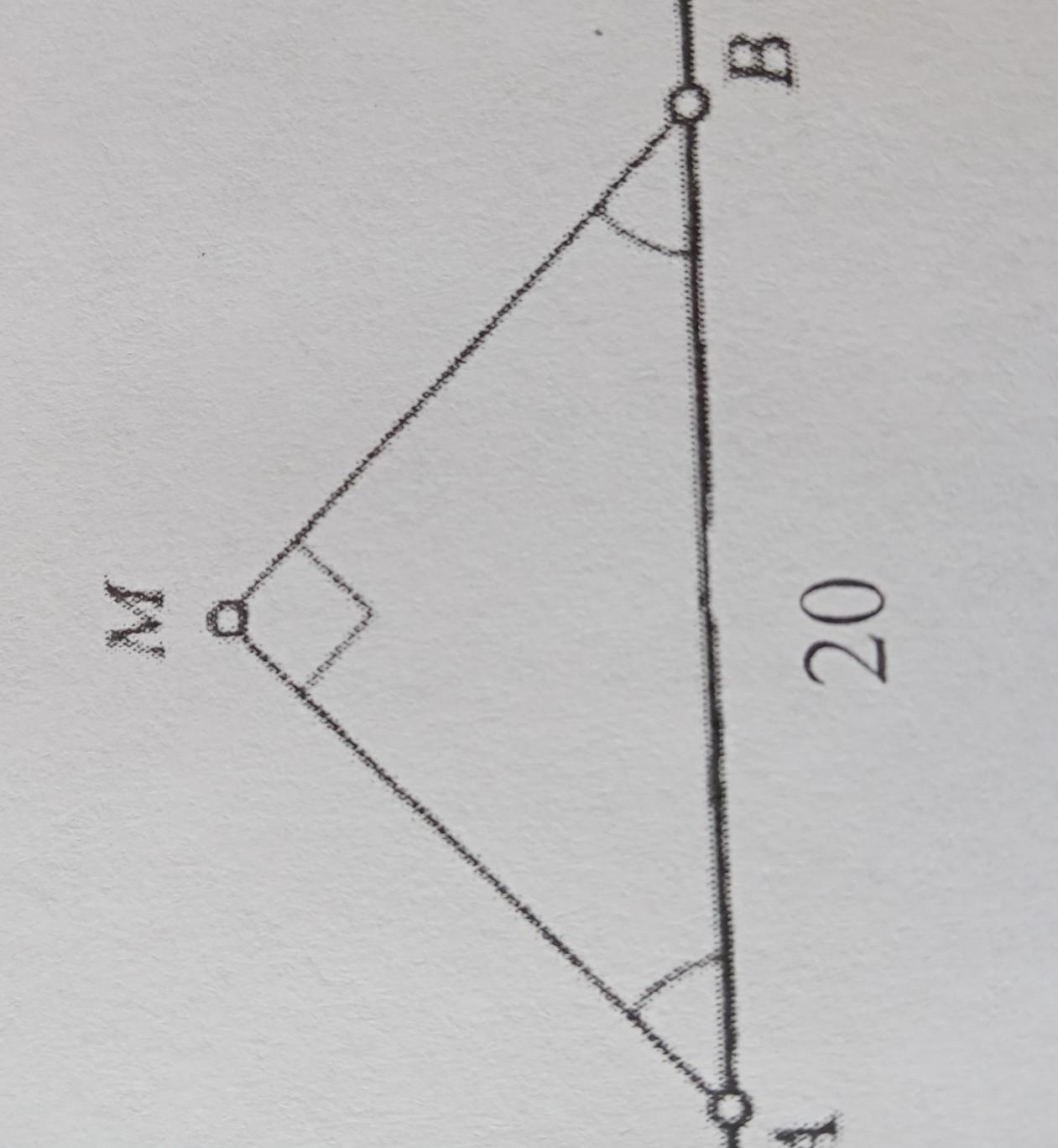
А Задание 5. Найдите расстояние от точки M до прямой AB. ​

Answer 1

Ответ:10

Объяснение:

углы при основании равны по 45°, катеты по 20*sin45°=20*√2/2=10√2

а искомое расстояние - это высота, проведенная из вершины М. и она равна √(1(100√2)²-(20/2)²)=10

высота проведена к основанию. потому она и медиана

Answer 2

Ответ:  10 .

Так как ∠АМВ=90° , то  ΔАМВ - прямоугольный . Гипотенуза АВ=20 .

Так как на рисунке обозначены равные углы ∠ВАМ=∠АВМ , то ΔАМВ является равнобедренным .

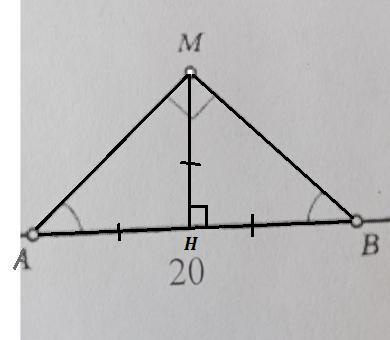
Расстояние от точки М до прямой АВ измеряется длиной перпендикуляра МН , опущенного из точки М на АВ .

МН - это высота, опущенная из прямого угла равнобедренного прямоугольного ΔАМВ на гипотенузу. Она является ещё и медианой . А медиана, опущенная из прямого угла на гипотенузу, равна половине гипотенузы, то есть МН=20:2=10 .