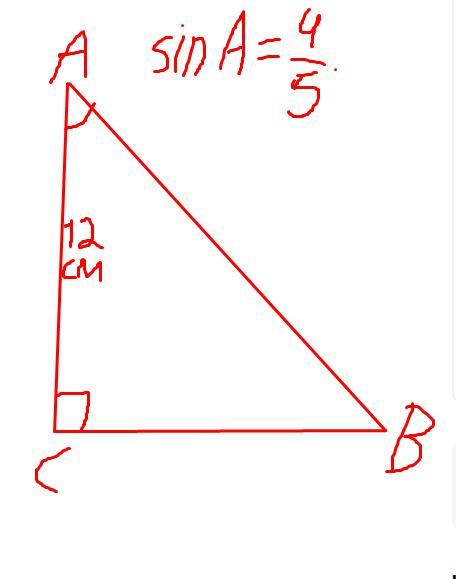
У ∆ABC ∠C = 90 , .
° AC = 12 см, sinA =4\5
Обчисліть : P ABC
Ответы
Ответ:
P ΔАВС=48 см.
Пошаговое объяснение:
Чертёж к решению прикреплён.
1) Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.
sin A=CB÷AB.
Ни СВ, ни АВ нам не дано, поэтому необходимо найти такую тригонометрическую функцию, которая будет оперировать известной стороной АС.
2) Это самой функцией будет косинус. Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.
cos A=АС÷АВ, где АС=12 см.
3) Найдём косинус, зная основное тригонометрическое тождество:
sin=√1-cos²α, откуда
cos=√1-sin²α.
За α примем ∠А. sin A=4/5=0,8. Итак:
cos=√1-sin²А.=√1-0,8²=√1-0,64=√0,36=0,6.
4) cos A=0,8=АС÷АВ=12÷АВ.
Через выражение 12÷АВ=0,6 можно выразить
АВ=12÷0,6=20 см.
5) Мы знаем АС=12 см и АВ=20 см, но не знаем ВС. Однако это исправимо, если воспользоваться Теоремой Пифгора:
АВ²=ВС²+АС², откуда можно выразить
ВС²=АВ²-АС²,
ВС²=20²-12²,
ВС²=400-144,
ВС²=256,
ВС=√256=16 см.
6) Периметром треугольника называют сумму длин его сторон.
Тогда Р ΔАВС=АВ+ВС+АС=20+16+12=48 см.