Question

2. Стороны треугольника равны 15; 24 и 18дм. Определите вид треугольника и найдите длину медианы, проведенной к меньшей стороне и радиус описанной около треугольника окружности.​

Answer 1

AB=15, AC=18, BC=24

Найдем больший угол A (против большей стороны BC) по т косинусов:

BC^2 =AB^2 +AC^2 -2AB*AC*cosA

cosA =(15^2 +18^2 -24^2)/2*15*18 = -1/20

Косинус угла A отрицательный - угол больше 90°.

Треугольник тупоугольный.

СM - медиана, AM=15/2

AMC, т косинусов:

CM^2 =AM^2 +AC^2 -2AM*AC*cosA

CM =√(15^2/4 +18^2 +2*15*18/2*20) =15√7/2

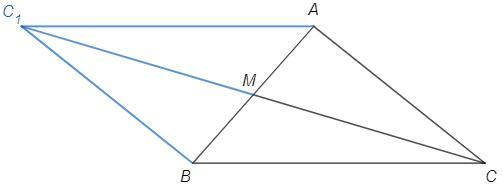
Или достроим до параллелограмма

В параллелограмме сумма квадратов сторон равна сумме квадратов диагоналей.

2(AC^2 +BC^2) =(2CM)^2 +AB^2

CM =√(2(18^2 +24^2)-15^2)/2 =15√7/2

ABC, т синусов

BC/sinA =2R

sinA =√(1 -cosA^2) =√399/20

R =24*20/2*√399 =240/√399