Предмет: Алгебра,
автор: natali908z
90 баллов произвольный треугольник имеет 2 равных угла третий угол в этом треугольнике равен 42° из равных углов проведены биссектрисы Найди меньший угол который образовывается при пересечении биссектрис
Ответы
Автор ответа:
1
Ответ:
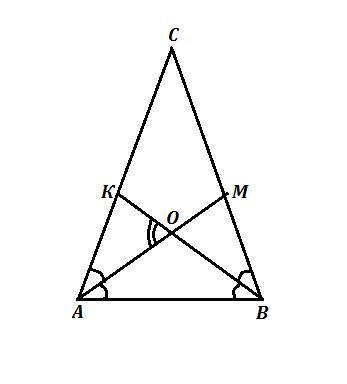
ΔАВС , ∠С=42° , ∠А=∠В ⇒ треугольник равнобедренный .
∠А= ∠В=(180°-42°):2=69°
АМ= биссектриса ∠А , ВК - биссектриса ∠В .
Известно , что все биссектрисы Δ пересекаются в одной точке, обозначим её буквой О .
Рассмотрим ΔАОВ . Так как ∠ОАВ=∠ОАК= ∠А:2=69°:2=34,5° и
∠ОВА=∠ОВМ= ∠В:2=69°:2=34,5° , то ∠ОАВ=∠ОВА . Значит ΔАОВ равнобедренный и его внешний угол ∠АОК= ∠ОАВ+∠ОВА=69° . Это меньший угол, образованный при пересечении биссектрис. (больший угол ∠АОВ=111° - тупой ) .
Приложения:
natali908z:
ответ не верен а я ждала ответ 35.5 тест кончился а ответ не верен
ответ верен
если ты не понимаешь, как решать, то ты не можешь судить о правильности решения... если хоть капельку есть разума, то прочти решение и поймёшь, что всё верно
Похожие вопросы
Предмет: Русский язык,
автор: Кристина2811
Предмет: Қазақ тiлi,
автор: Лейла9999
Предмет: Русский язык,
автор: Artem77sr
Предмет: Қазақ тiлi,
автор: baisangyr