Предмет: Алгебра,
автор: krapes404
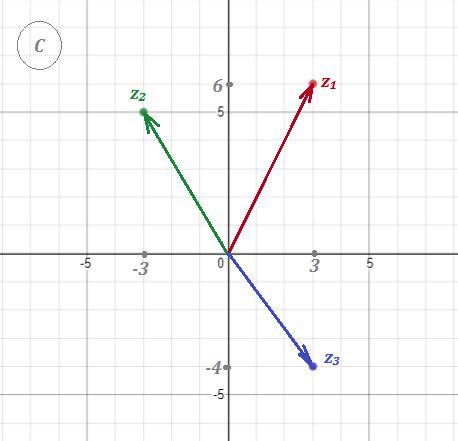
даны заданные в алгебраической форме комплексные числа: z1=3+6i z2=-3+5i z3=3-4i
1.изобразите на плоскости эти числа
2.найти произведение z1 на z2
3.найти частное от деления z3 на z2
Ответы
Автор ответа:
1
Ответ:
1) Cмотри рисунок .
3) Деление комплексных чисел. Умножим числитель и знаменатель на число, сопряжённое знаменателю .
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: Улан01
Предмет: Английский язык,
автор: мангл089
Предмет: Русский язык,
автор: kistochka2
Предмет: Биология,
автор: BogdanKL
Предмет: Английский язык,
автор: sofi099