Question

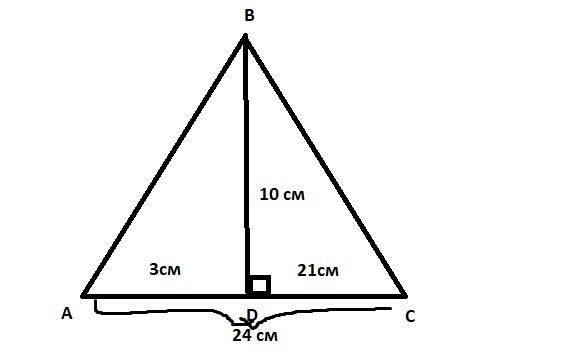
Дан треугольник ABC, на стороне AC которого взята точка D такая, что AD=3 см, а DC=21 см. Отрезок DB делит треугольник ABC на два треугольника. При этом площадь треугольника ABC составляет 120 см2. Найди площадь большего из образовавшихся треугольников, ответ дай в квадратных сантиметрах.
СРОЧНО!!!!!!!!!!!!!!!!!!!!!!!!!

Answer 1

Решение:

1. DB - высота треугольника, проведенная к основанию  AC

По формуле нахождении площади треугольника найдем высоту  DB:

S (ABC) =1/2 ah

(а - основание треугольника; h - высота)

120 = 1/2 (21+3) DB   DB = S/ AC 1/2

DB = 10 см

2. Рассмотрим треугольник  DBC. Высота, упавшая на основание AD, образовала прямой угол. Следовательно треугольник DBC прямоугольный. По формуле площади прямоугольного треугольника вычислим площадь  DBC:

S (DBC) = 1/2 a * b (значение a и b - катеты)

S (DBC)  = 10 см * 21 см /2 = 105 см2

Ответ: 105 см2