Предмет: Алгебра,
автор: 7atapael
Сложная задача за 9 класс, cos, tg, sin
Приложения:
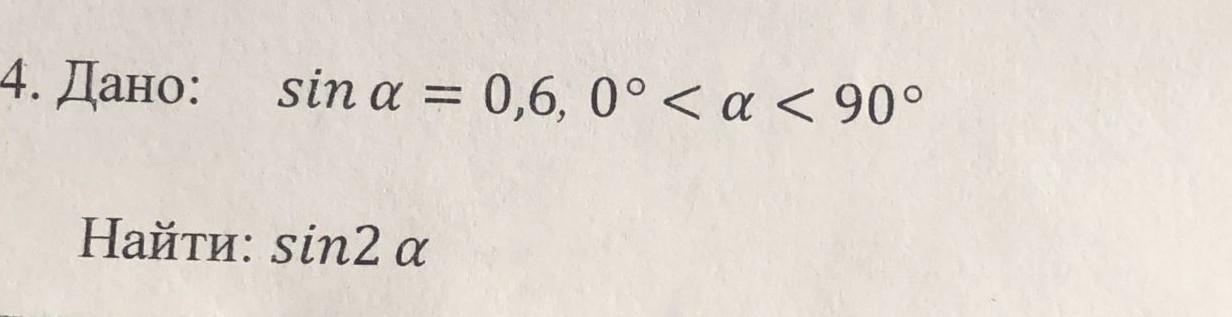
Ответы
Автор ответа:
2
Дано:
Найти:
Решение: Основное тригонометрическое тождество:
⇒ Так как угол α принадлежит l четверти, косинус будет неотрицательным. Найдем его.
- Формула синуса двойного угла:
⇒
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: гость133
Предмет: Русский язык,
автор: Равьям1
Предмет: Другие предметы,
автор: kitakat47
Предмет: Английский язык,
автор: Аноним