Дана функция y = 2х³-3х² Найдите: a) производную функции; b) критические точки функции; c) промежутки возрастания и убывания функции
Ответы
Ответ:
a) y' = 6x² - 6x;
b) х = 0 и х = 1 - критические точки;
c) Функция возрастает на промежутках х ∈ (-∞; 0] и на х ∈ [1; +∞), а на х ∈ [0; 1] функция убывает.
Объяснение:
(xⁿ)' = nxⁿ⁻¹
Производная от разности равна разности производных.
a) Найдем производную функции:
y' = (2х³ - 3х²)' = 2 · 3x³⁻¹ - 3 · 2x²⁻¹ = 6x² - 6x
b) Найдем критические точки:
Критические точки – это точки в которых производная функции равна нулю или не существует.
Прировняем полученную производную к нулю:
6x² - 6x = 0
6х(x - 1) = 0
х(x - 1) = 0
х = 0
х - 1 = 0
х = 1
х = 0 и х = 1 - критические точки.
c) Найдем промежутки возрастания и убывания функции:
Если у' > 0, то функция возрастает на данном промежутке, y' < 0 - функция убывает на данном промежутке.
Рассмотрим неравенство:
6x² - 6x > 0
6х(x - 1) > 0
х(x - 1) > 0
Решим методом интервалов. Найдем нули функции:
х = 0 и x = 1
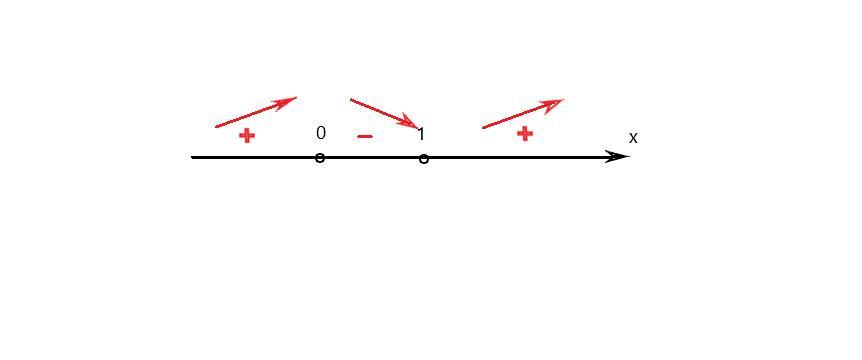
Отметим полученные точки на координатной прямой (см. вложение) и выясним знак производной на каждом из полученных промежутков.
при х ∈ (-∞; 0) ⇒ х(x - 1) > 0
при х ∈ (0; 1) ⇒ х(x - 1) < 0
при х ∈ (1; +∞) ⇒ х(x - 1) > 0
Поскольку функция непрерывна во всех критических точках, то они также входят в промежутки монотонности.
Функция возрастает на промежутках х ∈ (-∞; 0] и на х ∈ [1; +∞), а на х ∈ [0; 1] функция убывает.