Предмет: Алгебра,
автор: 1uUwUu1
используйте свойства соответствующих функций и решите уравнение
Приложения:
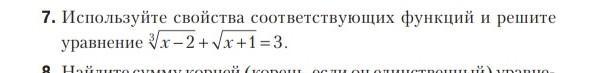
Ответы
Автор ответа:
1
Universalka:
Половина задания не отпечаталась. Сейчас допишу .
Можно было решить и так : в левой части возрастающая функция, в правой части постоянная, значит уравнение имеет не более одного корня . Затем найти корень подбором.
большое спасибо
Пожалуйста
Похожие вопросы
Предмет: Английский язык,
автор: Marely
Предмет: Беларуская мова,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: ariana3879