Предмет: Геометрия,
автор: versachexdior
геометрия #11
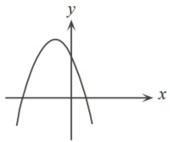
Если, на рисунке дается график функции y=ax2+bx+c, какое из следующих чисел всегда положительное?
Приложения:
Ответы
Автор ответа:
1
Ответ:
Всегда положительно число с
Объяснение:
Смотрим на график. Обращаем внимание на место пересечения графика с осью Оу.
Точка пересечения графика с осью Оу - это точка с координатами (0;у(0)), т.е. значение координаты (у) в этой точке равно значению функции при х=0
Эта точка находится выше нуля. Следовательно, в данной точке у>0
т.е. при х=0, у>0
Значение функции y=ax²+bx+c при х=0
Т.е. при таком графике функции всегда положительным будет свободный член, т.е. число c
versachexdior:
СПАСИБО ВАМ БОЛЬШООЕ❤
варианты: ab²; b-a; bc; c-a, какую выбрать?)
с - а
Поясню. Всегда положительное - с
Плюс к тому, у данной параболы ветви - вниз. А это означает, что коэффициент при х² всегда отрицательный
т.е. а < 0; с > 0
с - а = с + (-а); с > 0; (-а) > 0
с > 0, -а > 0 => с + (-а) > 0 <=> с - а > 0
а понятно
вы очень хорошо объясняете даже лучше
Похожие вопросы
Предмет: Русский язык,
автор: feel4
Предмет: Английский язык,
автор: Valdex
Предмет: Русский язык,
автор: Аноним
Предмет: Химия,
автор: danilsumin03
Предмет: Английский язык,
автор: masa766