ССССССРРРРРРРРОООООЧЧЧЧННННООООО!!!!!!!!!
докажите пж 1,2 и 3 задачу
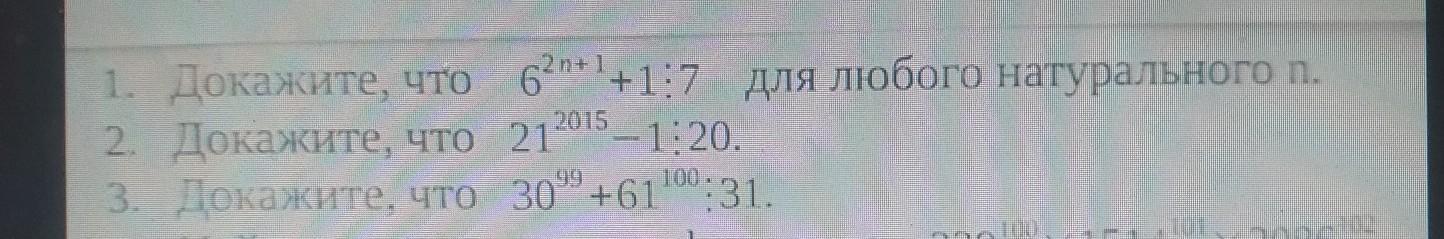
Ответы
a^n - b^n = (a - b)(a^(n-1) + a^(n-2)*b +.....+ a*b^(n-2) + b^(n-1))
3) 30^99 + 61^100 = 30^99 + 61*61^99 = 30^99 + 62*61^99 - 61^99 =
= 62*61^99 - (61^99 - 30^99) = 62*61^99 - (61 - 30)(61^98 + 61^97*30 +....+61*30^97 + 30^98) = 31*2*61^99 - 31 *(61^98 + 61^97*30 +....+61*30^97 + 30^98)
первый член кратен 31, второй кратен 31 ⇒ разность кратна 31
чтд
2) 21^2015 - 1 = (21 - 1)*(21^2014 + 21^2013 + ....+ 21 + 1) = 20*(21^2014 + 21^2013 + ....+ 21 + 1)
в произведении один из множителей кратен 20 ⇒ и произведение кратно 20
1) 6^(2n + 1) кратно 7
примением метод математической индукции (ММИ)
при n = 1 6^(2 + 1) + 1 = 217 кратно 7
пусть верно при n = k 6^(2k + 1) + 1 кратно 7
докажем что верно при n = k + 1
6^(2(k + 1) + 1) + 1 = 6^(2k + 3) + 1 = 36*6^(2k + 1) + 35 - 35 + 1 = 36*(6^(2k+1) + 1) - 35
первый на 7 делится так как 6^(2k+1) + 1, а 35 = 5*7 ⇒ и разность кратна 7