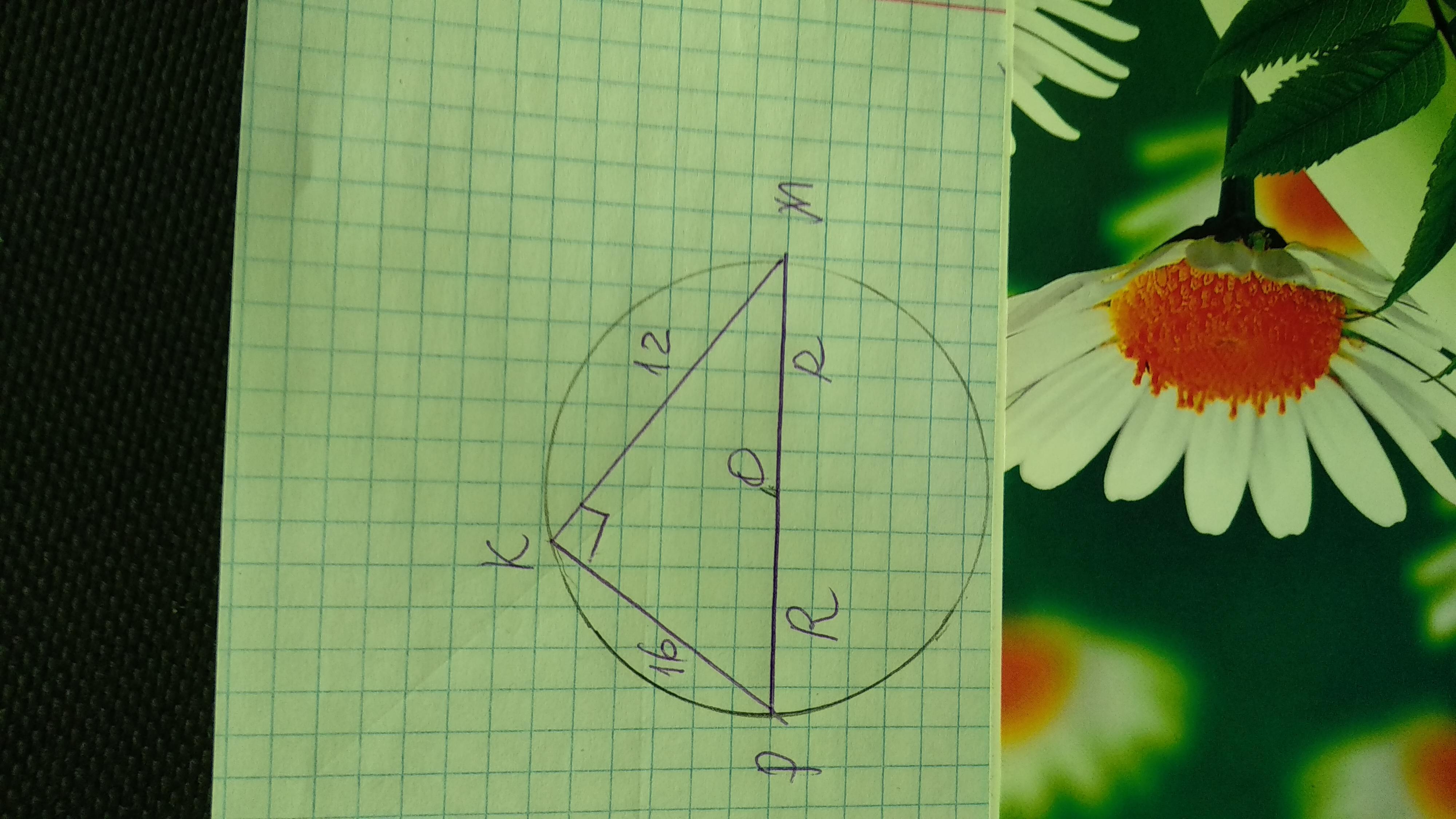
MKP - прямоугольный, K = 90, KM = 12, KP = 16. Найдите радиусы описанной и вписанной окружностей
( Обязательно полное решение с черчением ! )
Ответы
Ответ:
10 ед, 4 ед.
Объяснение:
Дано: ΔМКР, ∠К=90°, КМ=12, КР=16. R - ?; r - ?
По теореме Пифагора МР=√(КМ²+КР²)=√(144+256)=√400=20.
Радиус описанной окружности равен половине гипотенузы
R=20:2=10.
r=(a+b-c)/2=(12+16-20)/2=8/2=4.
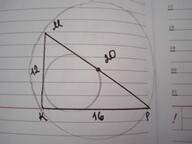
Ответ: 10; 4
Объяснение:
Дано:Δ МКР
∠К=90°;
КМ=12
КР=16
___________________________
Найти R, r
представим такую картинку - у нас есть прямоугольник со сторонами 12 и 16, чему равна диагональ? Верно, по Пифагору она равна
√(12²+16²)=√400=20
а вокруг этого прямоугольника описана окружность. Чем является ее радиус? половиной диагонали, поскольку диагонали пересекаются и в точке пересечения делятся пополам. значит, если вытереть один треугольник, на который прямоугольник разбивает диагональ, то получим треугольник, описанный около окружности, с тем же радиусом. поэтому ответ на первую часть вопроса 20/2=10
что касаемо второй части, есть множество формул для нахождения радиуса вписанной окружности.
например; √((р-а)(р-b)(h-c)/р), р=Р/2=(20+12+16)/2=(10+8+6)=24
r=√(((24-20)*(24-12)(24-16)/24)=√(4*8*12/24)=√16=4
или так:(КМ+КР-РМ)/2=(12+16-20)/2=6+8-10=4