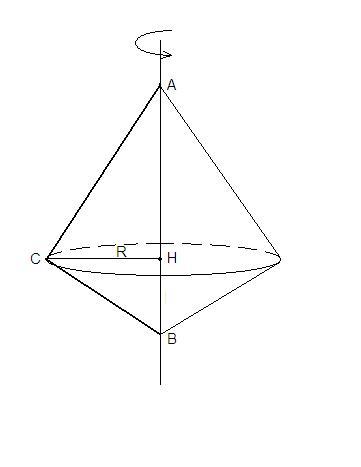
Прямоугольный треугольник с гипотенузой 12,5см и проведенной к ней высотой 6см вращается вокруг гипотенузы.Найдите площадь поверхности тела,полученного при вращении.
подробное решение с рисунком,пожалуйста

Ответы
Ответ:
105π см²
Объяснение:
При вращении прямоугольного треугольника вокруг гипотенузы получается тело, состоящее из двух конусов с общим основанием.
Высота, проведенная к гипотенузе, - СН - радиус основания конусов.
R = 6 см
Образующие конусов равны катетам прямоугольного треугольника АС и ВС.
Найдем катеты прямоугольного треугольника.
- Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению отрезков, на которые высота разбила гипотенузу.
Пусть АН = х - больший из отрезков , ВН = 12,5 - х.
СН² = АН · ВН
6² = x·(12,5 - x)
36 = 12,5x - x²
x² - 12,5x + 36 = 0 | ·2
2x² - 25x + 72 = 0
D = 25² - 4·2·72 = 625 - 576 = 49
x₁ = (25 + 7)/4 = 32/4 = 8
x₂ = (25 - 7)/4 = 18/4 = 4,5
АН = 8 см, так как переменной обозначен больший из отрезков.
ВН = 12,5 - 8 = 4,5 см
ΔАСН: ∠АНС = 90°, по теореме Пифагора
АС = √(АН² + СН²) = √(8² + 6²) = √(64 + 36) = √100 = 10 см
ΔВСН: ∠ВНС = 90°, по теореме Пифагора
ВС = √(ВН² + СН²) = √(4,5² + 6²) = √(20,25 + 36) = √56,25 = 7,5 см
Площадь поверхности полученного тела равна сумме площадей боковых поверхностей этих конусов:
Sпов. = S₁ + S₂
S₁ = πR·AC = π · CH · AC = π · 6 · 10 = 60π см²
S₂ = πR·BC = π · CH · BC = π · 6 · 7,5 = 45π см²
Sпов. = 60π + 45π = 105π см²