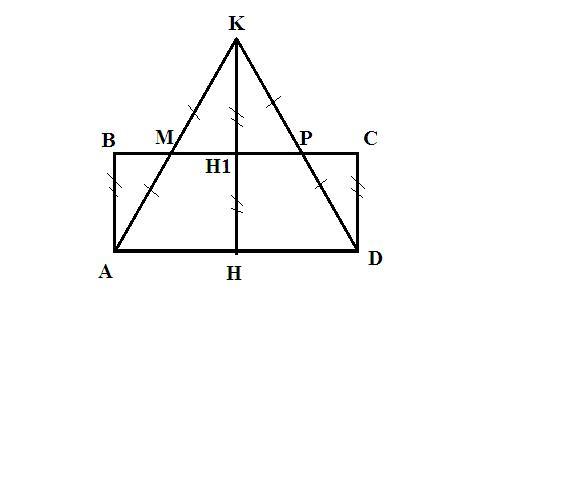
докажите что прямоугольник ABCD и треугольник AKD изображённые на рисунке равновеликие и равноставленные если MP средняя линия
ПОМОГИТЕ ПОЖАЛУЙСТА!!
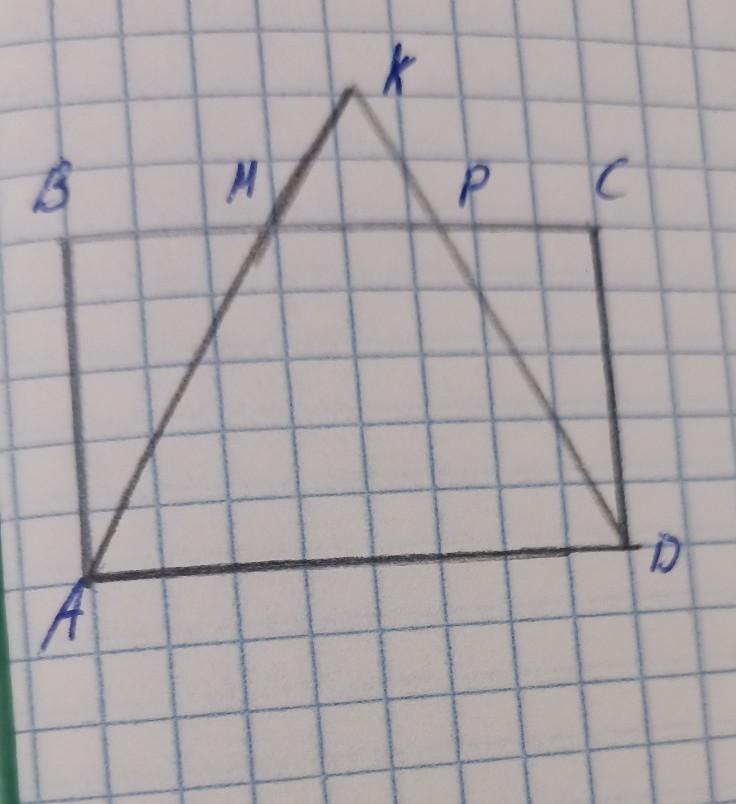
Ответы
Ответ:
Равновеликие фигуры – это фигуры с равной площадью.
Допустим AD=BC=a и AB=CD=b.
Площадь прямоугольника ABCD:
S=ab
MP – средняя линия, а она параллельна основания, что является прямой. Значит ΔADK – равнобедренный с равными боковыми сторонами AK=DK и основанием AD.
Средняя линия равна половине параллельного основания, значит MP=a/2
И BM=CP
BM+CP=a/2 (a/2, потому что если отнять BC-MP=a-a/2=a/2)
BM=CP=a/4
Средняя линия делит боковые стороны пополам, поэтому AM=MK и DP=PK. Так как у нас равнобедренный треугольник AM=MK=DP=PK.
Угол C – прямой. По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
PD²=CP²+CD² (CP=a/4, CD=b)
Значит боковая сторона равна
Опустим высоту KH. Высота равнобедренного треугольник является медианой тоже, поэтому AH=DH=a/2
По теореме Пифагора
KD²=DH²+KH²
KH²=KD²-DH²
Формула площади треугольника:
У нас a – сторона (у нас это AD), h – высота к этой стороне (в нашем случае KH)
Площадь прямоугольника тоже был ab
Значит ab=ab, следовательно они равновеликие.
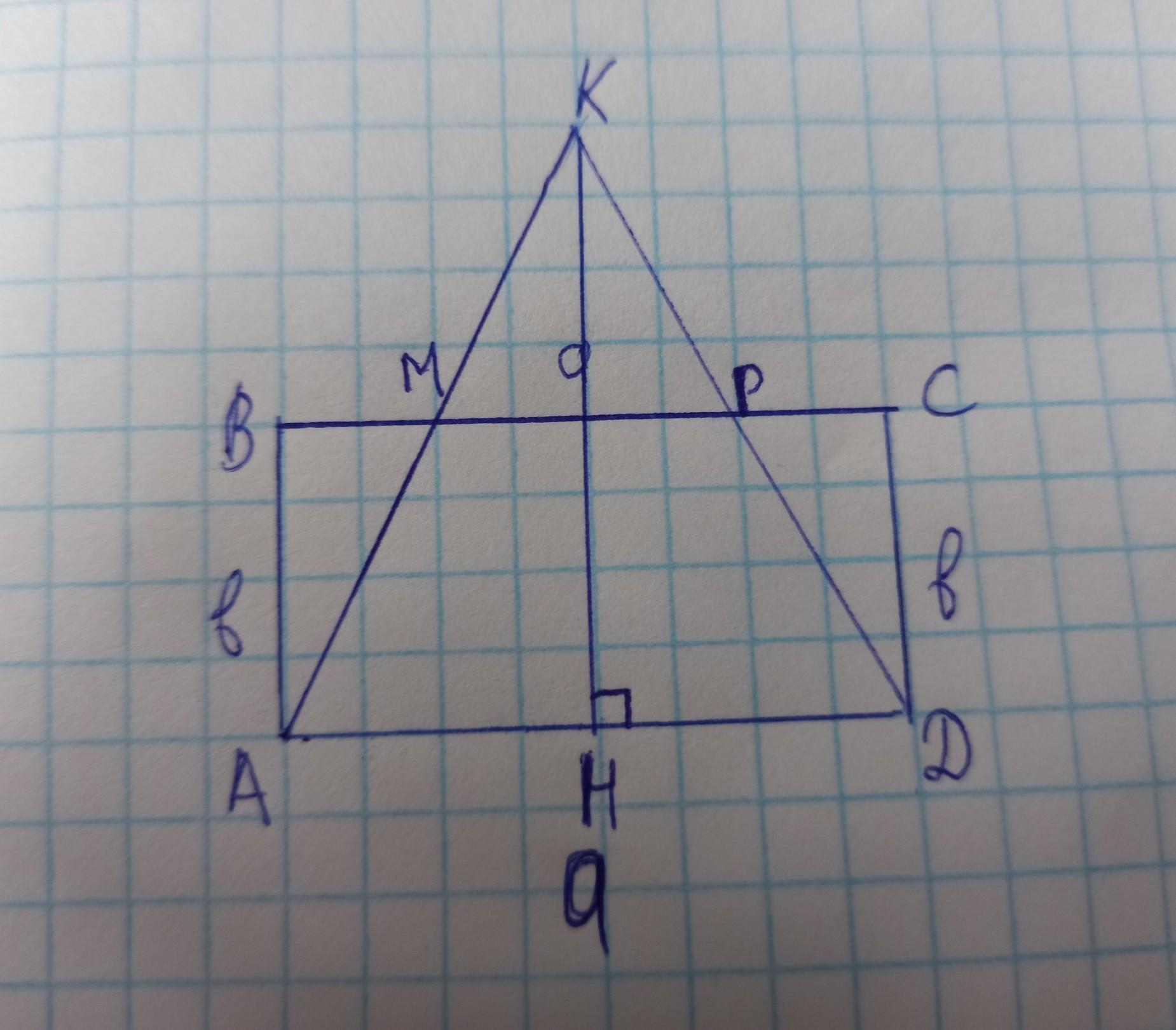
Ответ:
Объяснение:
Площадь треугольника S=ah/2, ⇒ S=AD*KH/2;
площадь прямоугольника S=a*b, ⇒ S=AD*AB;
МР - средняя линия ⇒ КН1=НН1=АВ=КН/2 ⇒ Sabcd=AD*KH/2=Sakd.