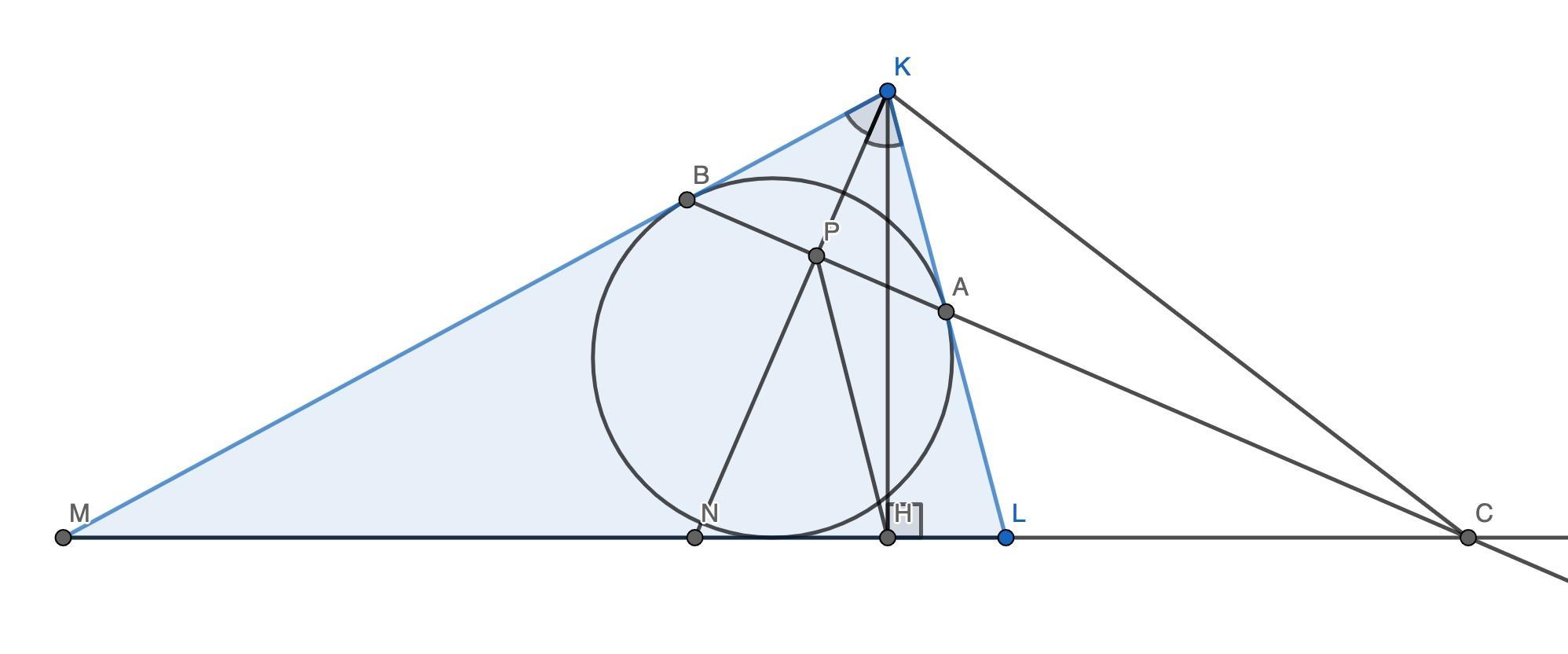
В треугольнике KLM сторона KM больше KL.
а) Докажите, что угол между высотой и биссектрисой, проведёнными из вершины K, равен полуразности углов L и M.
б) Окружность, вписанная в треугольник KLM, касается сторон KL и KM в точках A и B соответственно, KH - высота треугольника. Прямые AB и LM пересекаются в точке C. Найдите расстояние между точкой H и серединой отрезка AB, если уголKLM = 72 градуса, KML = 12градусов, CK= 24см.
Ответы
Ответ:
б) 12 см
Объяснение:
а) Пусть ∠L = α, ∠M = β. Тогда ∠K = 180° - (α + β), ∠LKN = ∠K / 2 = 90° - (α + β) / 2, ∠LKH = 90° - α, ∠HKN = ∠LKN - ∠LKH = 90° - (α + β) / 2 - (90° - α) = α - (α + β) / 2 = (α - β) / 2, что и требовалось доказать.
б) Отметим середину P отрезка AB. Треугольник AKB равнобедренный, так как AK = KB как отрезки касательных, проведённых из одной точки. KN — биссектриса треугольника AKB, значит, она проходит через середину AB, то есть P ∈ KN.
∠HKN = (72° - 12°) / 2 = 30° по доказанному в пункте а). Тогда ∠KNH = 90° - ∠HKN = 90° - 30° = 60°.
Поскольку AKB — равнобедренный треугольник, KP — биссектриса и медиана, KP также и высота, то есть ∠CPN = 90°. В прямоугольном треугольнике CPN ∠NCP = 90° - ∠KNH = 90° - 60° = 30°.
По теореме об угле в 30°: в треугольнике KNH KN = 2NH, в треугольнике CPN CN = 2NP.
По теореме косинусов: PH² = NP² + NH² - 2·NP·NH·cos∠KNH, CK² = KN² + CN² - 2·KN·CN·cos∠KNH = 4NH² + 4NP² - 2·4·NH·NP·cos∠KNH = 4·(NP² + NH² - 2·NP·NH·cos∠KNH) = 4PH² ⇒ CK = 2PH ⇒ PH = CK / 2 = 24 см / 2 = 12 см.