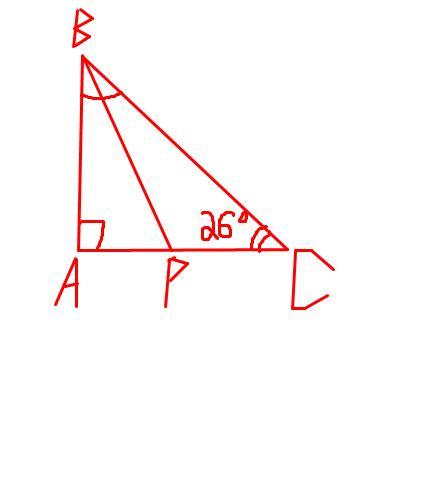Найдите большой угол между биссектрисой острого угла прямоугольного треугольника и противоположным катетом, если второй острый угол равен 26 градусов. Помогите решить пожалуйста. Срочно‼️‼️‼️
Ответы
Ответ:
∠СРВ, равный 122°.
Объяснение:
Чертёж к решению прикреплён.
Обозначим данный треугольник как ΔАВС с биссектрисой Р.
1) Известно, что ∠С=26°, тогда найдём ∠В, зная, что сумма углов треугольника составляет 180°: ∠В=180°-∠А-∠С=180°-90°-26°=64°. Итак, ∠В=64°.
2) Биссектриса — это луч, исходящий из вершины угла и делящий его пополам. По определению, ∠АВР=∠РВС=∠В:2=64°:2=32°.
3) Необходимо найти больший угол, образованный за счёт проведения биссектрисы от противолежащего катета по отношению к ∠В. Это либо ∠АРВ, либо ∠СРВ.
4) Для начала определим, что ∠АРВ+∠РВС=180°, так как они имеют общую сторону, проведённую от прямого отрезка.
5) Рассмотрим полученный ΔАРВ: ∠А=90°, ∠В=32°, тогда ∠Р=180°-90°-32°=58°.
6) Теперь рассмотрим оставшийся ΔРВС: ∠В=32°, ∠В=26°, тогда ∠Р=180°-32°-26°=122°.
7) 58°<122°, где 58°=∠АРВ; 122°=∠СРВ, следовательно ∠АРВ<∠СРВ.